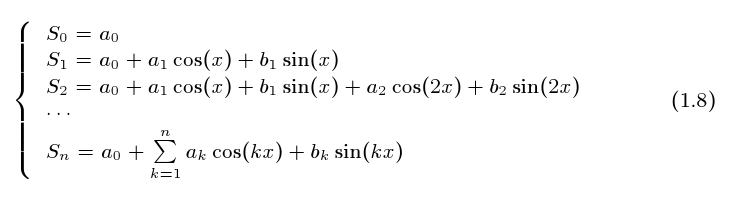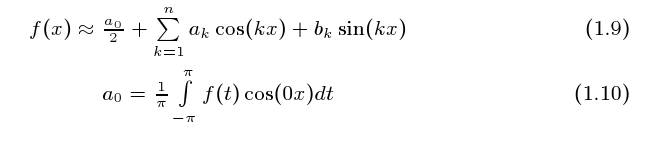Palavras chave:
coeficientes de Fourier, integral de Fourier, Polinômio trigonométrico,
transformada de Fourier.

O assunto de despedida
Estamos encerrando a disciplina, infelizmente eu não fui a fundo em alguns tópicos que
apenas iniciei como as integrais de superfícies em que eu deveria ter chegado a dois
teoremas fundamentais, de Gauss e de Stokes. Mas nem tudo poderia ser visto, e cheguei
perto deles com o que fizemos com o teorema de Green. Com algum esforço você pode
terminar este tópico e ver estes dois teoremas.
Se você consultar o planejemanto da disciplina verá que não inclui estes dois teoremas
como objetivo, eu temia que não houvesse tempo de chegar até eles de forma bem
fundamentada como fizemos com o Teorema de Green. Verá que todos os tópicos a que
eu me propunha foram estudados com suficiência de detalhes e de exercícios.
Ficou faltando um assunto, que é o que agora vou discutir:
séries de Fourier.
Vou evitar de fazer referência à terminologia série, porque ela exigiria
uma discussão que não
vou ter tempo de fazer, ficarei com a denominação polinômios trigonométricos
para a qual vou ter tempo suficiente.
Os polinômios trigonométricos estão associados, junto com outra transformação que
é bem semelhante a esta, com as nossas comunicações. Historicamente, até os anos 50
do século passado, eles eram a única forma de fazer comunicações (de codificar as
comunicações e transmití-las) por sua íntima associação com as ondas eletromagnéticas.
Hoje eles perderam um pouco deste espaço, seguem sendo a linguagem de máquina das
telecomunicações, que continuam sendo eletromagnéticas como meio, mas perderam o
espaço de codificação para outros métodos que foram construídos à imagem e semelhança
dos polinômios trigonométricos, em particular com uma transformação novíssima,
descoberta
(adquiriu o nome) em 1980, as wavelets, que são uma generalização
dos "polinômios
trigonométricos" no sentido de que as ondas básicas foram substituidas
por diversas outras que
melhor se adaptam ao tipo de objeto que se deseje codificar.
Antes, com os polinômios
trigonométricos apenas um tipo de onda básica era utilizada, o seno (o coseno é um seno
translatado) e as aceleradas do seno e do coseno.
Uma mulher, Daubechies, descobriu um tipo de
onda que tem uma adaptação muito
grande para a voz humana e para o ouvido humano, e com ela se pode decodificar
com maior precisão (com uma quantidade menor de amostras), transmitindo-se
uma quantidade pequena de informações para decodificar do outro lado e
obter uma reprodução muito mais perfeita (para a voz humana ou
para o ouvido humano).
O site de referência que associei na wikipedia ao nome de Daubechies lhe mostra que
haveria muito que fazer se eu fosse tentar reproduzir os métodos de comunicação e
portanto lhe mostrar que Cálculo serve para alguma coisa... ainda temos muito a andar
e construir na Universidade até que os nossos cursos possam estar mais próximos da
realidade
Isto não será possível, facilmente, porque os nossos governantes ,
quer dizer, aqueles
cujos salários nós pagamos para que eles administrem a coisa pública em nosso nome,
portanto nossos empregados,
estão muito afastados da realidade uma
vez que não compreendem como
é importante que o ensino conduza a nossa juventude a um domínio adequadamente
profundo das tecnologias.
Esta é a afirmação exata, eles vêm de um meio em que
estudaram
pouco e são em geral basicamente ignorantes de fato não
conseguem entender que o ensino é um investimento para a sociedade inteira.
Ganhariamos todos, inclusive eles, com um ensino bem estruturado e capaz de
conduzir o estudante a saber fazer. Para isto é preciso aliar o ensino teórico
com a prática e não dissociá-los criando Institutos de Ensino Aplicado....
Coeficientes de Fourier
Há uma forma bem simples de explicar o que são os coeficientes de Fourier.
É simples
logo se corre o risco de uma super simplificação deixando uma distorção no conceito.
Vou
procurar superar o risco.
Os coeficientes de Fourier são o "tamanho" da projeção de
uma função, uma onda
eletromagnética, por exemplo, na direção de uma onda básica,
uma senoide acelerada.
Vou trocar isto em miúdos.
As ondas básicas
Primeiro que tudo selecionamos algumas funções como sendo as mais
simples de um certo contexto. Você já viu isto no caso dos polinômios de
Taylor em que os polinômios (x - a)n foram
considerados os mais simples.
Então um polinômio de Taylor é uma
soma das combinações lineares das "projeções" de uma certa função
na direção das "ondas básicas"
Onda, aqui, eu estou usando como sinônimo de função! Uma onda eletromagnética é
uma função. A recíproca é que é difícil de aceitar, que qualquer função seja
uma "onda eletromagnética"... e realmente é uma afirmação discutível!
Discutível mas não é totalmente absurda!
Então os polinômios de Taylor são um vetor obtido como combinação linear de
vetores básicos, (x - a)n tendo como coeficientes o tamanho
da projeção de uma função f na direção destes vetores.
Esta comparação não é boa porque não temos o meio explicar esta projeção uma
vez que projeções estão associadas ao produto escalar entre dois vetores, e não
é este bem o caso dos polinômios de Taylor.
Apenas estou usando os polinômios de Taylor para começar a discussão porque eles
são muito cedo produzidos e apresentados nos cursos de Cálculo apesar de que
nem sempre os professores consigam transmitir a idéia de que eles estão associados
aos fênomenos da Álgebra Linear como combinação linear de vetores básicos com
coeficientes obtidos por uma certa operação - as derivadas sucessivas.
Quer dizer que eu estou procurando me inserir no contexto de um vetor
f e de sua
projeção num sub-espaço definido por uma coleção de vetores básicos (ondas básicas)
que no caso dos polinômios trigonométricos são senos e
cosenos acelerados:
sen( n t), cos(n t)
aqui a aceleração é o número inteiro positivo n.
Apenas para que você se conscientise de que estou tratando de coisas muito habituais,
você está acostumado a pensar que as cores são combinações de cores básicas (como
os polinômios de Taylor são combinações de funções básicas)
As ondas eletromagnéticas básicas
Vou deixar para trás os polinômios de Taylor e me concentrar no espaço vetorial gerado
pelas ondas básicas
sen( n t), cos(n t)
Um resultado fundamental
 uma conta relativamente fácil de fazer, tente, seja com mudança de variáveis, observando
que a derivada do sin(t) é cos(t), ou com propriedades geométricas, agora observando que
f(t) = sin(t) é uma função par e que g(t) = cos(t) é uma função impar , isto deve conduzí-l@ a
ver que esta integral é zero.
uma conta relativamente fácil de fazer, tente, seja com mudança de variáveis, observando
que a derivada do sin(t) é cos(t), ou com propriedades geométricas, agora observando que
f(t) = sin(t) é uma função par e que g(t) = cos(t) é uma função impar , isto deve conduzí-l@ a
ver que esta integral é zero.
Mas, tente os dois métodos, reveja um pouco do Cálculo I,
eu vou precisar que estes
conceitos estejam bem vivos em sua memória nesta nossa despedida de Cálculo II.
Estou usando, ao repetir a fórmula acima, a notação de produto escalar:
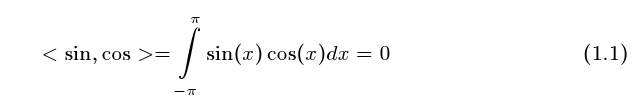
Podemos mostrar, e é possível que você tenha visto isto em Álgebra Linear,
que esta fórmula define um produto escalar.
É até bem possível que você tenha
imaginado que @ professor tenha inventado apenas uma fórmula a mais para lhe
causar problemas na prova, ou uma generalização gratuita do produto escalar entre
vetores do plano ou do espaço que serve, num visão geométrica fácil, para discutir
o ângulo entre vetores.
Bom, as funções são vetores, as funções do Cálculo são vetores de um
espaço de
dimensão não finita!
Nada de muito extranho nisto, um polinômio de grau cinco é um elemento de um
espaço vetorial de dimensão maior ou igual a cinco. Para conseguirmos boas aproximações
com polinômios de Taylor (de MacLaurin) das funções trigonométricas que você usa
quando aperta um botão de calculadora, precisamos de polinômios de Taylor de grau 17,
elementos de um espaço vetorial de dimensão maior ou igual a 17.
Você já está rodeado de objetos, de vetores, de espaços com dimenção alta! somente precisa
se acostumar com a idéia.
Nada disto tem uma tradução geométrica em termos de nossa prisão tridimensional, as
tentativas de fazer esta adaptação não resultam em nada muito interessante, sobretudo
porque o que nos interessa não é a dimensão quatro, mas sim, pelo menos, a dimensão
17.
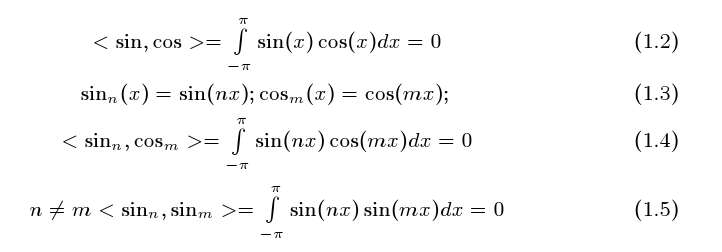
Quer dizer que qualquer seno acelerado é perpendicular a qualquer coseno acelerado, e
bem mais do que isto, qualquer seno acelerado é perpendicular a outro seno acelerado com
aceleração diferente.
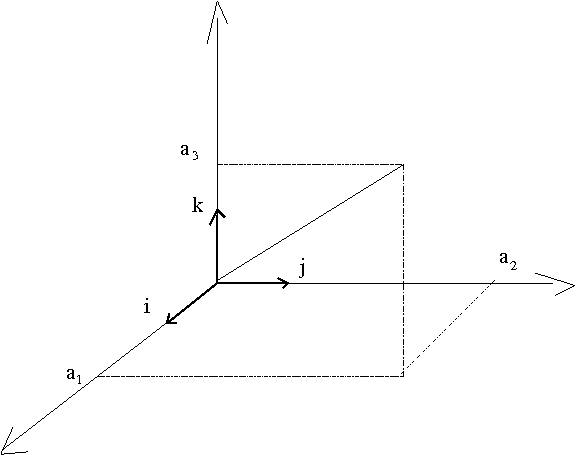
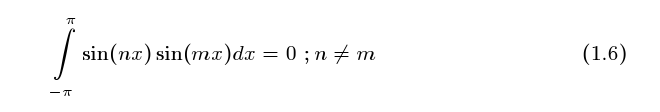 Para completar esta imagem que você já encontrou na Álgebra Linear, de uma
família de vetores perpendiculares, na verdade encontrou uma família de
vetores ortogonais generalizando os vetores i,j,k da Física, que são os vetores
Para completar esta imagem que você já encontrou na Álgebra Linear, de uma
família de vetores perpendiculares, na verdade encontrou uma família de
vetores ortogonais generalizando os vetores i,j,k da Física, que são os vetores
(1, ...,0), (0,1,...,0), .... (0,0,...,1)
tendo 1 em uma posição e zero nas demais.
Agora estou lhe mostrando que existe uma família de ondas eletromagnéticas, sen(nx),
sen(mx), cos(k x), cos(j x) que forma uma família não finita
de vetores perpendiculares
entre si.
Uma quantidade não finita de elementos básicos também já é do seu conhecimento com os
polinômios
(x-a)n
em que você tem uma família não finita de vetores linearmente indepentes formando uma
base para um espaço vetorial de dimensão infinita.
Agora você tem outra família não finita de vetores linearmente indepentes formando uma
base para um outro espaço vetorial de dimensão infinita o espaço das ondas
eletromagnéticas.
Entretanto eu ainda preciso fazer mais ajuste neste conjunto de vetores, na verdade, se
trata de corrigir o produto escalar. Vou inserir uma escala.
Os vetores básicos não são unitários
Consideramos isto um defeito, que os vetores básicos, que compõem a base do espaço vetorial,
não sejam unitários.
Se justifica facilmente este "preconceito"! Queremos os vetores básicos para representar
os outros vetores do espaço com os elementos da base.
Por exemplo, considere os vetores i, j , k da Física. Eles são unitários!
Se não fossem observe a complicação que isto iria produzir:
- u = a1i +
a1j +
a1k
representa um vetor do espaço, como combinação linear de
i,j,k
- se eu quiser a projeção de u na direção de i
calculo o produto escalar:
- <u, i>
<a1i + a1j +a1k,
i> =
= a1
Porque < i , i > = 1.
Deixo que você faça as constas que pulei! Se você não fizer as contas, não irá aprender!
- Use a distributividade do produto escalar
relativamente à soma;
- que o produto escalar entre diferentes vetores do conjunto
{ i,j,k}
é zero, porque estes vetores são perpendiculares entre si;
- e, finalmente, que o produto escalar de qualquer vetor do conjunto
{ i,j,k}
com ele mesmo é 1 porque eles são unitários.
A última sentença contém um conteúdo relativo! É o que me interessa aqui.
Os vetores
da Física, i,j,k são unitários relativamente
ao produto escacalar
que costumamos usar!
Então as integrais que calculei acima entre senos e cosenos são um produto escalar e
preciso redefinir este produto escalar para que os vetores sin, cos tenham
módulo 1.
Fique alerta, existem muitas definições de produto escalar, escolhemos a que nos
interessa para um determinado objetivo. Isto pode parecer confuso, mas com o tempo
você verá que não é.
A definição de produto escalar que me interessa é
![produto escalar em [-pi, pi]](exer14/exer14_00_05.png)
e você pode calcular e verificar que |sin| = |cos| = 1.
Não somente o módulo do sin, cos é 1 como também o os módulos de qualquer das
aceleradas.
Calcule! estas integrais são fáceis, se deduzem direto da relação
fundamental da trigonometria junto com o fato de que seno e coseno são translatadas
uma da outra.
Quer dizer que temos uma sucessão de vetores de módulo 1, perpendiculares entre si,
ou seja uma base de vetores ortonormais com uma "quantidade" não finita de elementos,
portanto uma base para um espaço vetorial de dimensão não finita!
Intrigante, entretanto, é que não podemos fazer nada com "quantidades" infinitas, os
nossos computadores não suportam este tipo de situação, e a unica solução para podermos
usar este "novo" (no começo do século 20 era novíssimo) sistema é se consideramos uma
projeção do sistema em um espaço de dimensão finita, mesmo que de dimensão grande.
Quanto maior a dimensão mais precisos serão os nossos resultados (e mais lentos irão
rodar os nossos programas) o que forçou uma série de melhorias ao longo do século 20
criando as possibilidades que temos hoje de comunicações rápidas - desde que as privadas
que nos exploram permitam, obviamente o que os desgovernantes que
nos infestam permitam esta exploração.
Sim, nossas comunicações poderiam ser velocíssimas, porque temos os meios hoje.
As comunicações são codificação e decodificação.
Quando escrevi um vetor como combinação linear dos vetores
i,j,k
da Física, eu codifiquei o vetor u:
u = a1i +
a1j +
a1k
e agora posso dizer que
u = ( a1,
a1,
a1)
e você está tão acostumado com esta forma de escrever que sua primeira reação será
de que estou dizendo bobagem! Ora, isto são apenas as coordenadas do vetor u.
Verdade! mas mude o sistema de coordenadas, altere os vetores básicos!
Estou vendo que você meneia a cabeça me dizendo que "sim", verdade!
A seleção de um sistema de vetores básicos é uma convenção (um código) que me permite
enviar apenas a lista de coordenadas por e-mail e do outro lado o meu correspondente
cria a mesma imagem:
que estou vendo aqui.
Se eu fosse enviar a imagem o tempo de processamento (neste grande supercomputador
que é a rede) seria muito maior do que o um e-mail contendo apenas a frase:
As coordenadas do vetor u são (3,4,7)
Supondo que ambos estejamos com um terminal do gnuplot em nosso trabalho comum,
estaremos vendo simultaneamente a mesma imagem diante de nós.
Isto funciona porque os dois usamos o mesmo sistema de codificação, os vetores
i,j,k da Física. Então é suficiente enviar o código (3,4,7) que
tem alguns dados que fazem parte da codificação:
é um terno ordenado.
então não pode haver dúvida, veremos o mesmo desenho.
O programa
fourier.gnuplot vai criar o
código. Rode o programa e procure
entender o que ele faz.
O código são as coordenadas do vetor f na direção dos vetores básicos sin(kx), cos(kx),
obtidas pelos produtos escalares:
- ak = < f , cosk >
- bk = < f , sink >
com o produto escalar que defini acima.
Na versão do programa que se encontra na página, f(x) = (x+3)*(x-3)
é uma função par, e você pode ver que os coeficientes bk são todos
próximo de zero.
- a0 = -5.70987943278033
- a1 = -4.00050486686586 ;b1 = 7.97368483435946e-07
- a2 = 1.0005048663239 ;b2 = -1.59473924387325e-06
- a3 = -0.444949309864821 ; b3 = 2.39211459025088e-06
- a4 = 0.250504864155539 ; b4 = -3.18949680571469e-06
- a5 = -0.160504862529361 ;b5 = 3.98688818107321e-06
- a6 = 0.111615971652812 ; b6 = -4.78429100749045e-06
- a7 = -0.0821375112538629 ; b7 = 5.58170757125528e-06
- a8 = 0.0630048554821572 ; b8 = -6.37914016603116e-06
- a9 = -0.049887568459547 ; b9 = 7.17659108009266e-06
- a10 = 0.0405048489766943 ;b10 = -7.97406260676743e-06
- a11 = -0.0335626964213861 ; b11 = 8.77155703682958e-06
- a12 = 0.0282826188029269 ;b12 = -9.5690766597472e-06
- a13 = -0.024173475560263 ; b13 = 1.03666237676382e-05
- a14 = 0.0209129948925525 ;b14 = -1.11642006535679e-05
- a15 = -0.0182826041635681 ; b15 = 1.19618096079539e-05
- a16 = 0.0161298207826342 ;b16 = -1.27594529255333e-05
- a17 = -0.014345645267548 ;b17 = 1.3557132899037e-05
Deveriam ser exatamente zero - mas o programa calcula aproximadamente
as integrais. Isto traduz o fato de que f é uma função par, logo suas componentes
ao longo dos vetores sink são nulas.
Se eu usar a linguagem da Física (ou da música), eu vou dizer que os harmônicos
de f nas frequências de sink são nulos.
Esta é uma frase típica de que faz análise espectral, e aqui você tem outra aplicação
dos polinômios trigonométricos - a análise espectral,
que vai permitir identificar elementos
a partir dos coeficientes dos sinj ou cosk que se pode detectar
quando as ondas que eles emitem ao serem estimulados por certas emissões de energia.
Porém aqui estou falando de coisas de que entendo pouco, e que você irá estudar com
técnicos da área quando se envolver com algumas dessas aplicações:
- comunicações
- análise espectral de material
para citar apenas duas áreas de aplicações dos coeficientes de Fourier e das integrais
de Fourier que é o nome que tem as integrais que calculam os coeficientes
ak, bj
Falta-me terminar a análise do que faz o programa fourier.gnuplot.
Rodando o programa você uma sucessão de gráficos, ele está mostrando os sucessivos
gráficos dos polinômios trigonométricos:
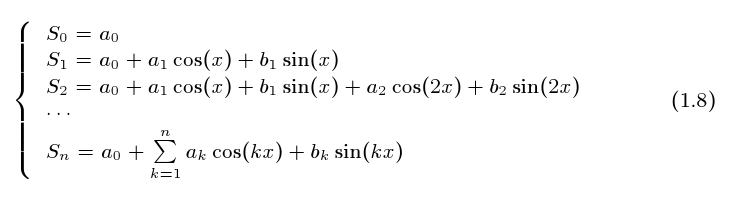
a medida que os coeficientes vão sendo calculados, cada vez que você acionar o
enter.
Era como se eu estivesse enviando uma sucessão de coeficientes para alguém
que então poderia ver a imagem, melhorando a cada acréscimo de coeficientes.
No gráfico você vê uma parábola que é aproximada apenas no intervalo [-pi, pi]
por um polinômio trigonométrico.
Chamar isto de aproximação é discutível!
Mas entenda o que estamos fazendo, ou que está ocorrendo.
- Primeiro uma parábola, f(x) = (x-3)(x+3)
não é uma onda eletromagnética;
- estou usando um sistema que é excelente para
codificar (e decodificar) ondas eletromagnéticas aplicado em alguma coisa que nada
tem de periódico, como são as ondas eletromagnéticas;
- Posso alterar o espaço onde são calculados os coeficientes de Fourier, usando
um intervalo qualquer [-T , T] e então posso ampliar a visão desta aproximação, mas
depois ela vai colapsar como a que você está vendo no programa, fora o intervalo;
- Entretanto, se f representar um fenômeno periódico a aproximação será perfeita com
alguns termos do polinômio trigonométrico.
Você pode melhorar sua intuição dos fatos trocando a função f no programa e voltando
a rodá-lo. Observe que no programa há dois pontos com o comentário:
####### altere aqui #######################################
em que lhe é dito que troque apenas a equação deixando "f(x) ="
- Por exemplo, troque
f(x) = (x+3)*(x-3)
por
f(x) = x+4;
e você irá ver os polinômios trigonométricos se aproximando de uma função que
chamamos de serrote.
- Troque
f(x) = (x+3)*(x-3)
por
f(x) = (2.0*x)(1.0 + x**2) ;
e você irá ver os polinômios trigonométricos se aproximando de uma figura bem
interessante ...
Um gráfico com gnuplot
Uma função recursiva, definida em gnuplot produz o polinômio trigonométrico facilmente
em casos em os coeficientes de Fourier tenham uma expressão recursiva. É o caso
com a função f(x) = x, cujos coeficientes de Fourier aparecem num dos itens do exercício
01 da lista 14, eles tem a forma simples (-1)(k+1)/k e eu montei
a função recursiva para produzir o polinômio trigonométrico:
S(x,n,k,soma)=(k==n)?soma:f(x,n,k+1,soma+(-1)**(k+1)*sin(k*x))
então o comando
plot f(x,30,1,sin(x)),x,0
produz o gráfico
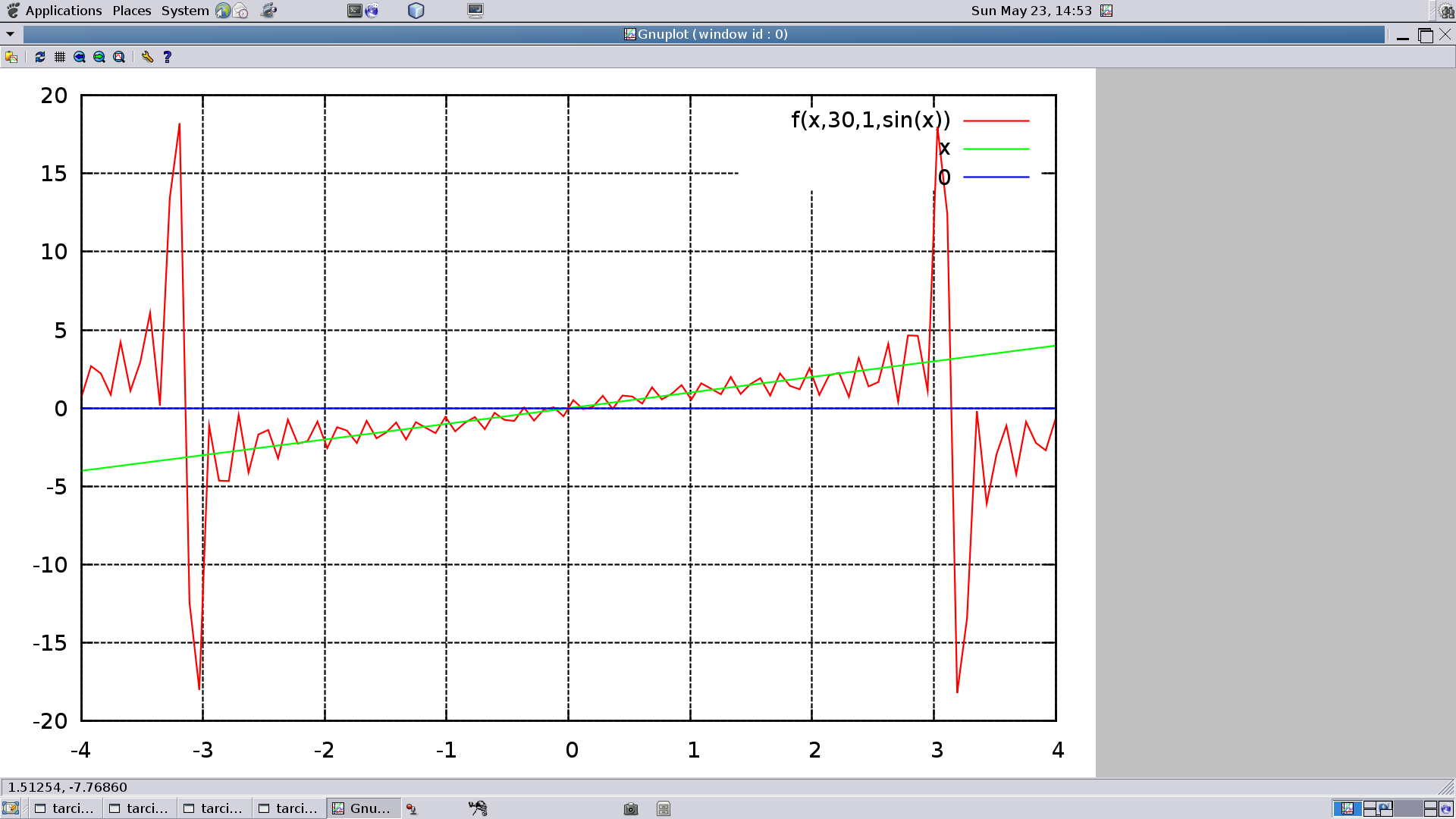
Os coeficientes a0 e b0
Este é um dos pontos bonitos da historia.
O coeficiente b0 é simplesmente zero porque ele reprsenta
a projeção de f na direção de sen(kx) quando k = 0, que é identicamente zero. Este
vetor é retirado da base porque na base não pode haver vetores nulos. Então
é simples, não há componente nesta direção e o coeficiente b0=0.
Se calcularmos o coeficiente usando a fórmula para ak,
com k=0, vamos observar um erro nos valores do polinômio
trigonométrico relativamente aos valores da função de quem eles devem ser
uma aproximação. Temos duas opções para corrigir o erro:
- alterar o produto escalar;
- alterar o valor de a0, usando a mesma expressão para o produto
escalar mas definindo como a0/2.
A preferência recaiu nesta segunda opção e a fórmula dos polinômios trigonométricos
se escreve assim:
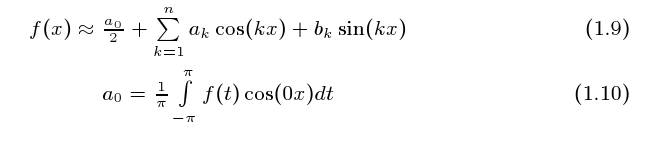
e você pode ver que a0 é o valor médio integral de f no intervalo considerado.
Se f for uma função contínua este valor médio coincide com o valor de f no ponto médio
do intervalo. Se f for descontínua este valor corresponde à média do salto que f tiver ai,
ou seja, o polinômio trigonométrico corrige a descontinuidade de f
da maneira melhor
possível.
Wavelets
Aqui entra um comentário para terminar.
Foi poristo que apareceram as wavelets, elas não surgiram repentinamente como
o texto sugere acima, em 1988, apesar de que se costuma citar um congresso da SIAM em
que Daubechies apresentou a sua descoberta recente, como um marco para o nascimento
das wavelets. Mas isto é uma brincadeira agradável e de certa forma uma honra ao
trabalho de Daubechies que produziu um instrumento de grande importância - uma onda
que não tem equação algébrica, mas que tem uma definição que se assemelha muito
à construção
de fractais, e se aplica na codificação da voz humana.
Este processo, que culminou em 1988, já vinha caminhando desde a década de 60,
(porém há trabalhos da década de 30 que já estavam caminhando nesta direção, ou
mesmo antes... tem quem inclua as wavelets de Haar de 1900) quando
se tentava "enjanelar" os polinômios trigonométricos para cortar o que acontecesse fora
de um intervalo e aos poucos foram sendo construidos processos que conduziram ao uso
de "pequenas ondas" já usadas por Yves Meyer durante os anos 80 que as chamava
de "ondeletes", (pequenas ondas em francês). Mas seria difícil de citar aqui uma grande
de pesquisadores que contribuiram para o nascimento das wavelets e para a quase
derrocada das transformadas de Fourier que nasceram com Euler no começo do século
18 e ganharam o nome de Fourier num trabalho que Joseph Fourier apresentou á Academia
Francesa de Ciências, em 1807, em que teve a ousádia de dizer que todas as funções
periódicas podiam ser colocadas como somas de senos e coseno, as séries de Fourier.
De certa forma resta um lugar seguro para os polinômios trigonométricos, o de
linguagem de máquina - codificar e decodificar ondas eletromagnéticas,
que, por enquanto,
é como sabemos transmitir as informações entre as torres e os satelites de comunicação.
Como se fazem as comunicações
Esta parte do texto é ficção científica, não a leve a sério, mas ela lhe vai dar algumas
informações sobre como se fazem as comunicações, quero dizer, sobre a linguagem
de máquina das comunicações...
Suponha que você e eu vivamos à margem de um lago suficientemente grande para que
não seja possível nos vermos, mas não tão grande que nos impeça de usar alguns
meios de comunicação rústicos, um sino para avisá-l@ que tenho uma comunicação
a fazer.


 uma conta relativamente fácil de fazer, tente, seja com mudança de variáveis, observando
que a derivada do sin(t) é cos(t), ou com propriedades geométricas, agora observando que
f(t) = sin(t) é uma função par e que g(t) = cos(t) é uma função impar , isto deve conduzí-l@ a
ver que esta integral é zero.
uma conta relativamente fácil de fazer, tente, seja com mudança de variáveis, observando
que a derivada do sin(t) é cos(t), ou com propriedades geométricas, agora observando que
f(t) = sin(t) é uma função par e que g(t) = cos(t) é uma função impar , isto deve conduzí-l@ a
ver que esta integral é zero. 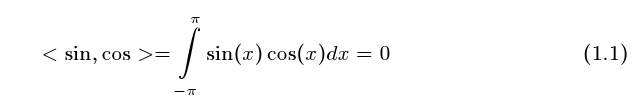
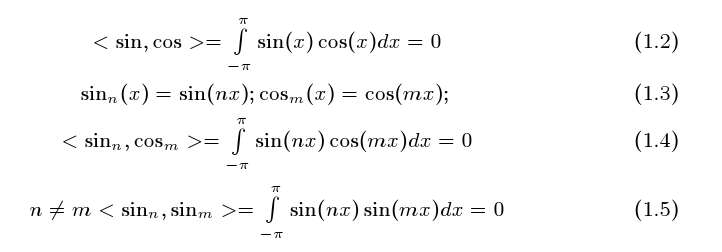
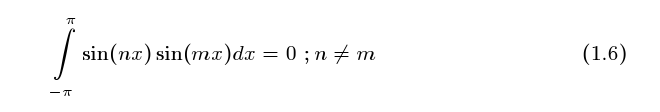 Para completar esta imagem que você já encontrou na Álgebra Linear, de uma
família de vetores perpendiculares, na verdade encontrou uma família de
vetores ortogonais generalizando os vetores i,j,k da Física, que são os vetores
Para completar esta imagem que você já encontrou na Álgebra Linear, de uma
família de vetores perpendiculares, na verdade encontrou uma família de
vetores ortogonais generalizando os vetores i,j,k da Física, que são os vetores![produto escalar em [-pi, pi]](exer14/exer14_00_05.png)