Palavras chave: baricentro, centro de massa,
comprimento de arco,
curvas, curvas sobre superfícies, derivada implícita,
integral de linha,
medida de objetos no espaço,
parametrização de curvas,
parametrização de superfícies, valor médio integral,
parametrizaçao de curvas, variedades.

Superfície, dimensão
Este texto serve de apoio às listas 04 e 04b que podem ser encontrada no
link "exercicios" da página do curso. Sempre observo que os textos de apoio
embora eu procure escrevê-los da forma mais completa possível, são insuficientes e
coloco palavras chave como um auxílio para que você complete a exposição com outros
textos que você pode encontrar na Internet ou em livros na biblioteca.
Eu já falei, rapidamente, a respeito de dimensão. Centrei a exposição na
existência de objetos no espaço com distintas dimensões - tanto os espaços
como os objetos.
Há uma forma intuitiva de entender dimensão e compreender uma dificuldade
básica que temos por nos encontramos imersos num espaço 3D com uma linguagem
oriunda da visão que os gregos tinham da geometria que se limita ao mundo 3D.
Costumo dizer que somos prisioneiros, culturalmente e energeticamente,
da terceira dimensão.
Com isto não podemos perceber, usando os instrumentos físicos que temos,
visão, tato, mesmo que o poder destes intrumentos naturais sejam muito
engradecidos por instrumentos construídos pelo homem,
nenhum objeto que se encontre fora da dimensão 3, e a linguagem
que herdamos na geometria, se limita à dimensão 3 embora faça referência a
objetos de dimensão 2 e 1.
O método que uso é experimental e intuitivo para adquirir em seguida um uso
formal destes conceitos mas sempre a partir de uma conceituação intuitiva
para andar mais rápido.
Entretanto tenho que observar que é Álgebra Linear que pode formalizar
corretamente o conceito de dimensão.
Uma palavra foi inventada para nos liberar desta prisão, variedade. Os
objetos da geometria se chamam variedades.
- Diremos uma variedade de dimensão 1, para fazermos referência aso
segmentos de reta, às retas, às curvas. Todos estes objetos são
variedades de dimensão 1.
- Quando me referir aos objetos de dimensão 2, direi variedades de
dimensão dois.
- Há uma grandesubclassificação das variedades - duas grandes
classes:
- As variedades lineares, segmentos de reta, retas, planos , as
variedade lineares de dimensão 3, 4 para as quais não temos mais nomes
geométricos.
- As variedades não lineares, um círculo, uma parábola, são dois
exemplos de variedades não lineares de dimensão 1. Uma superfície de
tipo parabolóide, as parabólicas podem ser pensadas como sendo tal, são
variedades não lineares de dimensão 2.
- Um ponto você pode classificar como quiser, uma variedade linear de
dimensão 0, ou uma variedade não linear de dimensão 0.
- Herdamos nomes particulares para alguns tipos de variedades de dimensão
1, círculos, retas, parábolas, ou simplesmente a palavra curva, uma
variedade de dimensão 1.
- Também temos nomes para algumas variedades de dimensão dois, plano,
superfície esférica. A palavra superfície quer dizer uma variedade de
dimensão 2.
- O espaço todo em que estamos imersos é uma variedade linear de
dimensão 3.
- O espaço-tempo da Física é uma variedade de dimensão 4. Linear?
depende, se o tempo tiver uma condição inicial, não! porque neste caso
seria um poliedro... poliedros, embora tenham fronteiras feitas de
subconjuntos de variedades lineares, não são mais variedades lineares.
- Observe que uma reta qualquer é uma variedade linear afim - isto
quer dizer, por exemplo, que a origem pode não pertencer a reta.
Se a origem pertencer à reta, ela é uma variedade linear. Se a
origem não pertencer á reta ela é uma variedade linear afim de dimensão
1.
- Quais serão as variedades lineares afins de dimensão 2 ?
Não se
assuste, vamos usar variedades e com o tempo você irá compreendê-las
bem.
Eu escrevo textos que têm o objetivo de ser pedagógicos na condução do leitor a dominar
Matemática e com isto nem sempre a linguagem é precisa. Por um lado é preciso que
@ leitor seja crítico e procure encontrar as imprecisões como parte do seu processo de aprendizado
e inclusive se comunique comigo para nesta discussão eu melhorar o texto ou e simplesmente
dirimir dúvidas. Tomo um exemplo simples, a lista 04b usa um "arame" como exemplo
de curva no espaço. Ora, um arame é um sólido, uma espécie de cilindro com uma diretriz
que algumas vezes não é retilínea, portanto uma variedade dimensão 3 com que estou
representando (dando exemplo) de uma variedade de dimensão 1. Portanto aqui há
um erro e é preciso que @ leitor esteja consciente do mesmo, embora eu o considere um
instrumento pedagógico o que inclue a crítica - a crítica faz parte do aprendizado.
Variedades de dimensão 1 imersas em variedade de dimensão 2 ou 3.
Um exemplo de variedades de dimensão 1 (curvas) podem ser imagens que
obtivermos de curvas no domínio projetadas sobre o gráfico de uma
função.
Há várias razões para que use estes exemplos, um deles: é um modo
fácil de obter uma curva no espaço.
Mas logo você vai ver que uma outra razão está no horizonte... a
palavra chave seria transformação. Posso ver a imagem mencionada acima
como uma transformação (deformação) de uma curva do plano - a sua
imagem no espaço. Ou vice-versa, a imagem recíproca da imagem de uma
curva no espaço deformada para obter uma curva plana.
Por enquanto deixe-me simplesmente construir imagens de curvas planas em
cima de superfícies no espaço. Vamos aprender a manipular tais
objetos.
A fórmula do comprimento de arco
A questão 02 da lista 04 conduz à fórmula do comprimento de arco.
Infelizmente eu cometi um erro que torna nulo (falso) o item (b) quando coloquei em
evidência a diferença
tk+1 - tk+1
quando devia ter escrito
tk+1 - tk
Em aula pedi que corrigissemos esta fórmula para aproveitar o trabalho e chegarmos à
fórmula correta que aparece no item (d) - a equação (8).
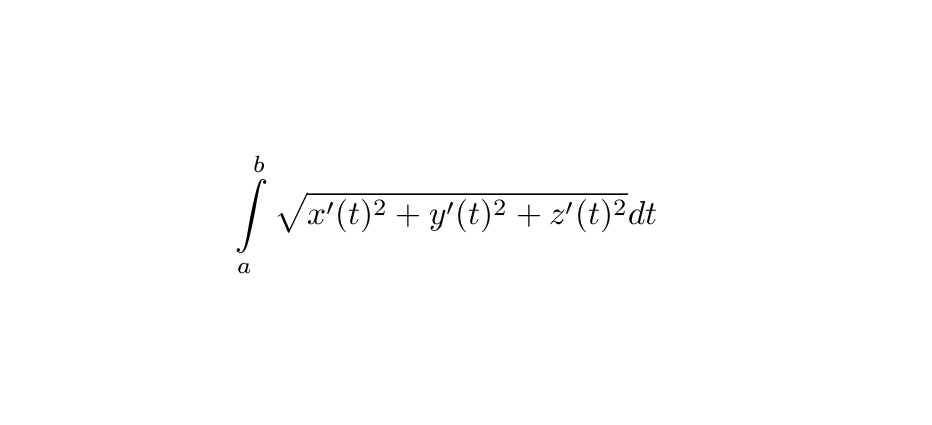
A expressão (corrigida em aula) do item (b) é uma soma de Riemann e as somas de Riemann tem como limite integrais que
podemos identificar calculando os dois limites de integração que ficam identificados pelas diferenças no parâmetro usado
no intervalo de parametrização da curva: definido na questão (1) item (b) - o intervalo [a,b].
A questão 03, lista 04.
Temos aqui uma função que pertence a uma classe importante entre as funções que servem para modelar pontos críticos. No
denominador está o quadrado do módulo do vetor (x,y) o garante que a origem não se encontra no domínio. Estas funções servem para
modelar a presença de buracos negros no Universo ( precisariamos de uma expressão um pouco mais complicada, mas esta
serve para começar). Os buracos negros são corpos com grande concentração de massa a ponto de absorverem toda radiação que se
encontre "muito perto" deles e consequentemente não há retorno
de "mensagens" enviadas a eles. O ponto (0,0) no gráfico desta função pode
representar, aproximadamente, um buraco negro, e este ponto não pertencde ao domínio da função uma vez que não podemos
calcular F(0,0).
O círculo unitário tem um papel importante no gráfico desta função, ele divide a superfície (graf(F)) em duas regiões com propriedades
bem semelhantes - ambas de natureza infinita. Numa destas regiões se encontra o polo (0,0, F(0,0)).
Observe que eu não disse o "ponto" e sim o "polo" - seria uma representação da presença de um buraco negro.
É muito difícil obter um 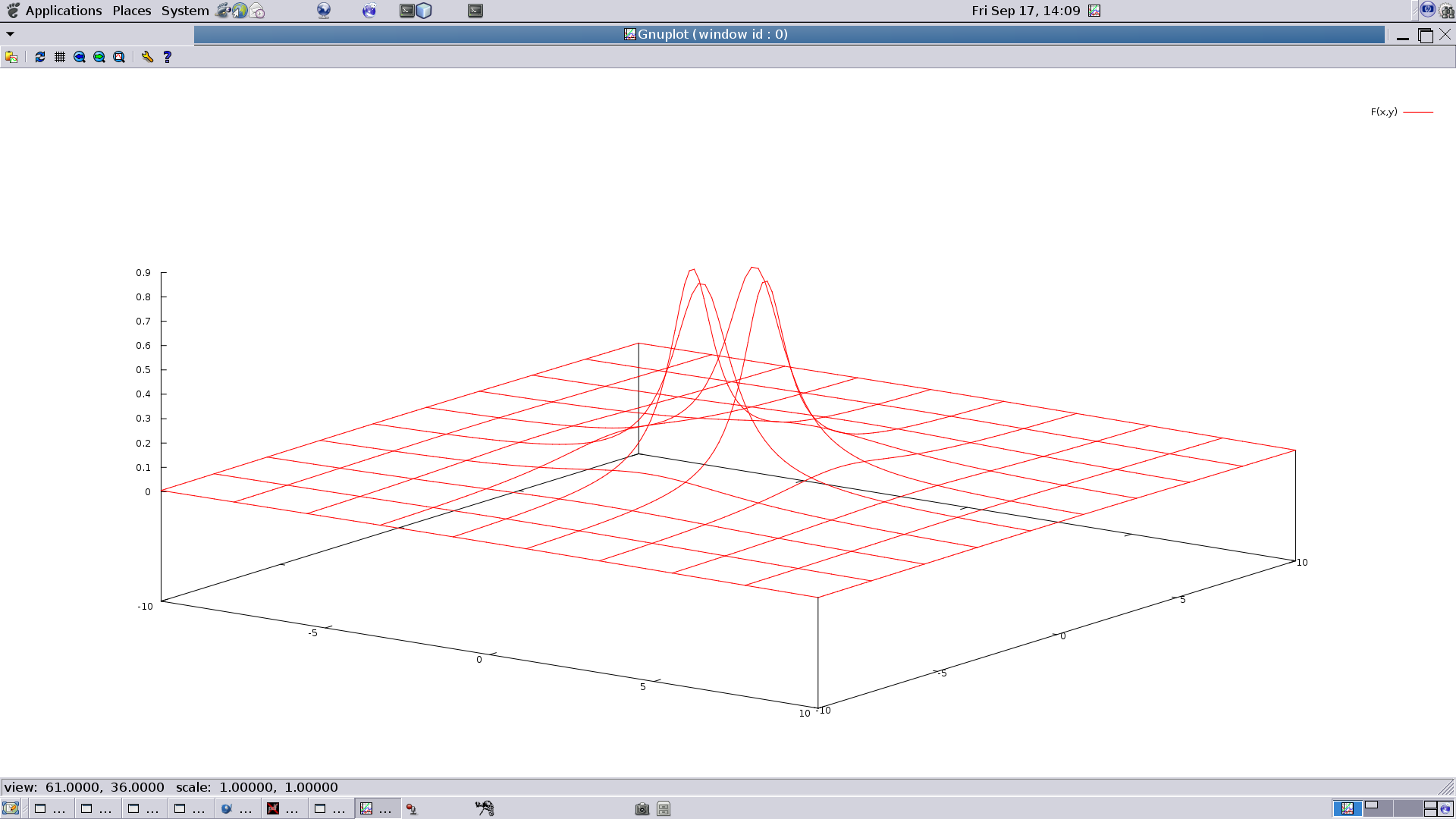 gráfico interessante desta superfície dentro do círculo unitário- imagem de S1 .
gráfico interessante desta superfície dentro do círculo unitário- imagem de S1 .
O gráfico acima foi feito com splot do gnuplot tendo como parâmetro a equação de F. Neste gráfico apenas fica sugerido que há um
problema no ponto (0,0)...
Os gráficos que seguem foram feitos com um programa em C++ que cria um arquivo de dados para gnuplot depois chamando gnuplot
para mostrar o gráfico. Neles aparecem a imagem do círculo unitário - objeto da questão 03-b) sobre a superfície.

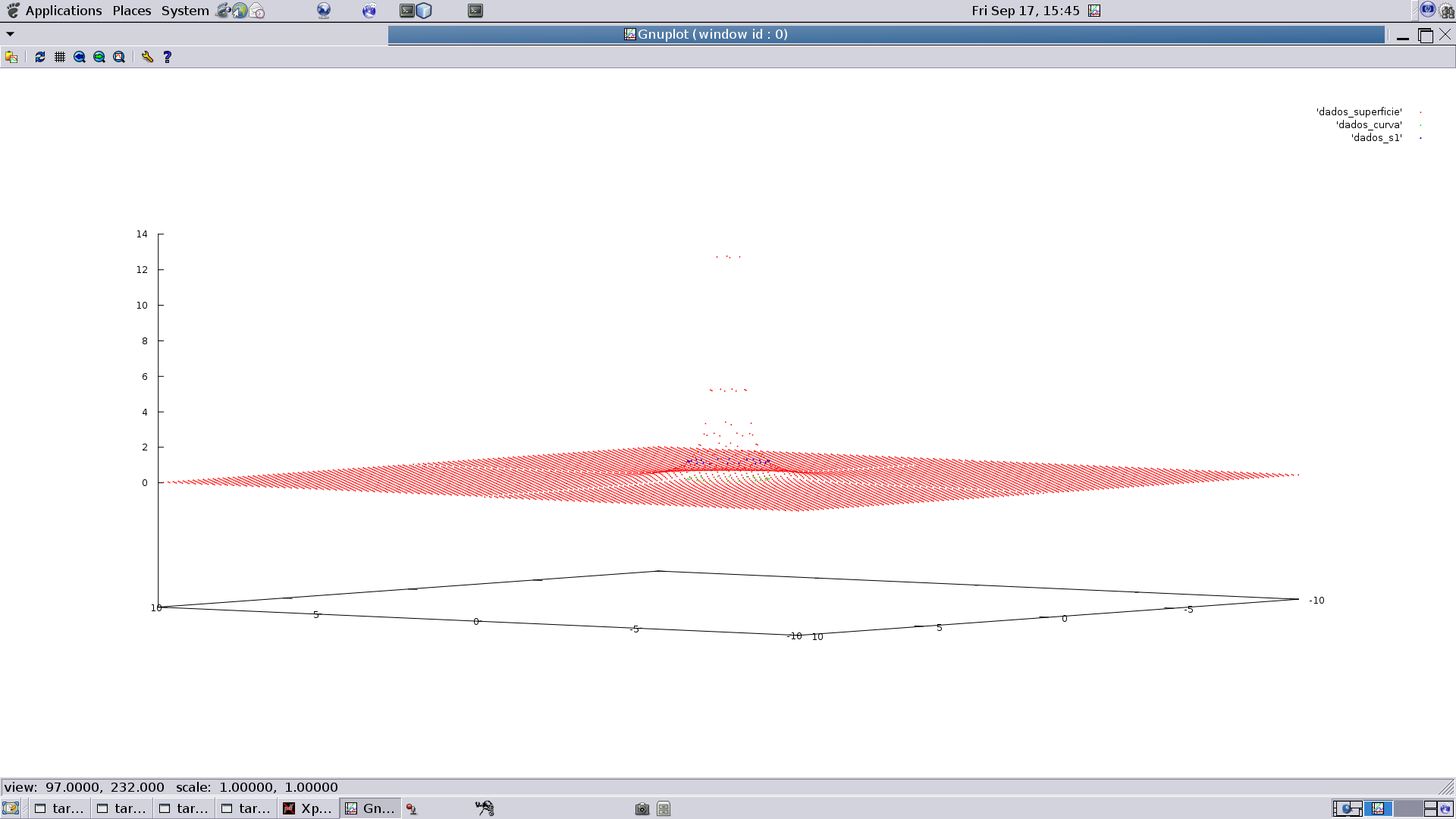
A imagem do círculo unitário sobre a superfície é um círculo unitário, precisamente porque o círculo unitário, no domínio de F
são os únicos pontos que que produzem o valor 1 quando F lhes for aplicada. Outra forma de dizer isto é que S1 é a curva
de nível 1 de F. Então o comprimento desta imagem é o comprimento de um círculo de raio 1 e assim um
dos itens b, c é o verdadeiro.
No item (d) não foi calculada a derivada z'(t) dentro da integral que calcula comprimento de arco: item errado.
No item (3), se a derivada z'(t) estiver correta então se tem o comprimento de arco da curva é a imagem de uma translação do
círculo unitário pelo vetor (-3,4)
Os dois gráficos seguintes foram feitos com uma versão mais recente do programa referido acima em que estou usando pequenos
segmentos de reta (segmentos de comprimento menor do que 1) tangentes à superfície. Com isto estou criando uma rede que simula o
formato da superfície.
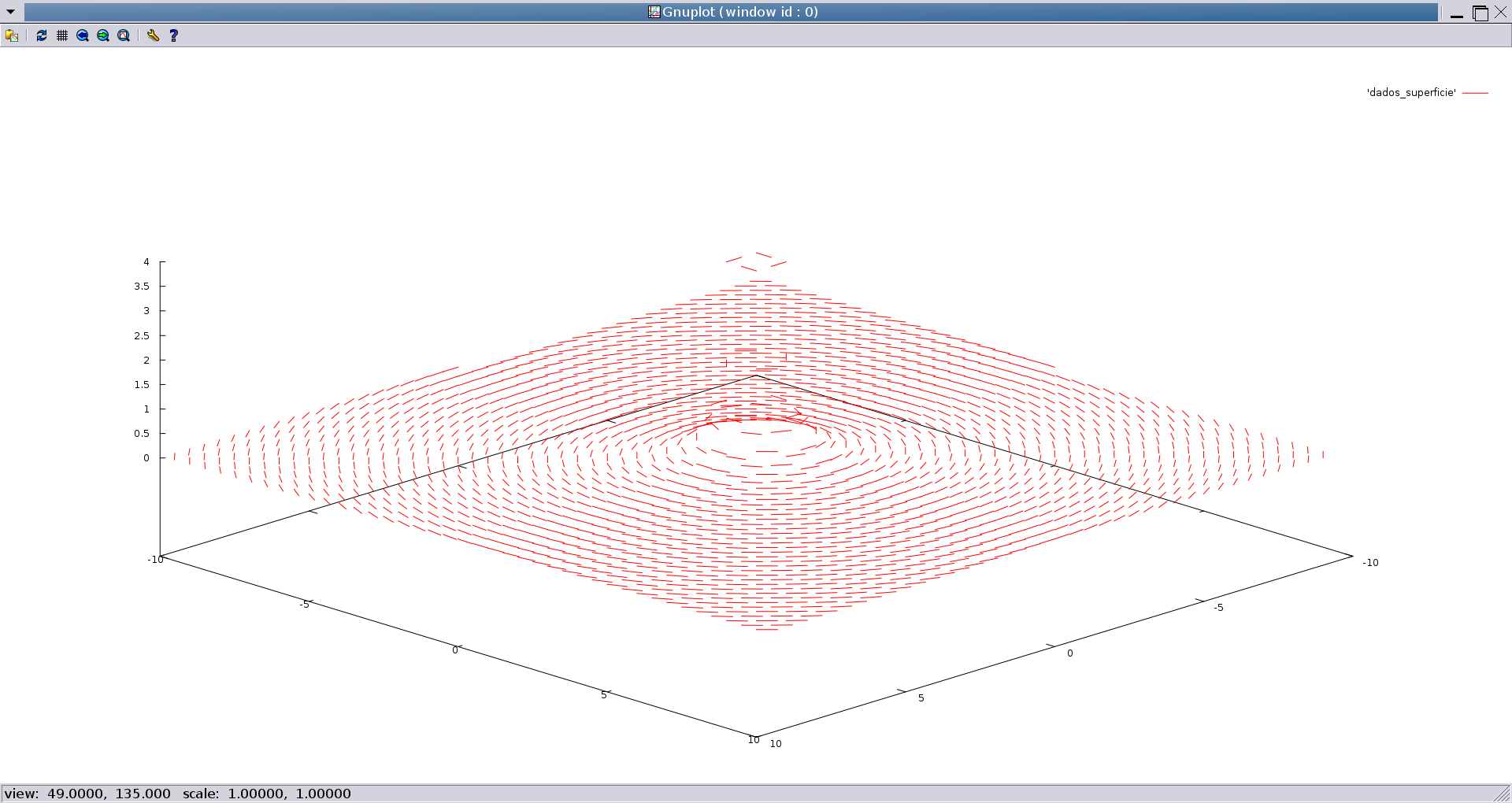
Estes gráficos foram gerados por um script do gnuplot que precisa
de um arquivo de dados onde se encontram
os segmentos de reta tangentes à superfície. Como gnuplot lhe permite produzir rotações no gráfico, é possível adquirir uma visão melhor
do formato da superfície diferente da visão estática dos gráficos acima. Experimente e se prepare para discutir o programa em aula na
quarta-feira e posteriormente produzir uma versão melhor do programa - é o objetivo.
Na verdade um dos objetivos e traduzir a dificuldade que existe para que possamos compreender o gráfico de uma superfície quando nós e as
superfícies nos encontramos no mesmo espaço... todos prisioneiros da dimensão 3. É preciso procurar uma estratégia que construa uma
linguagem gráfica que nos permita "ver" o gráfico da superfície. A estratégia que estou buscando é a construção da rede e você pode intervir
neste trabalho ajudando me a construir um programa melhor como forma de entender as técnicas do Cálculo que estará envolvidas na
construção do programa: derivada, segmentos de reta tangentes.
Vou mostrar, ao discutir o programa, que estou usando o gradiente de F para obter vetores tangentes à superfíce. Desta
forma não vou apenas falar de um conceito teórico, gradiente, vou mostrar que ele pode ser usado para obter objetos concretos.
Detesto a preocupação utilitarista que ela tem um viés consumista e portanto destrutivo do meio ambiente,
entretanto podemos admitir
utilitarismo como uma motivação para adquirir conhecimento.
É uma forma mais evoluida do utilitarismo que os
burocratas das chamadas agências de fomento não conseguem entender.
Integral de superfícies
Vou começar de leve a discutir a integral de superfícies. Elas são um pouco mais complicadas do que as "integrais de linha" como se
deve esperar porque vão ser integrais sobre variedades de dimensão dois e então mais trabalhosas dos que as integrais univariadas que
é o caso das "integrais de linha".
Com o tempo você vai ver que há alguma coisa escondida nesta dificuldade, lembre-se do que já falei anteriormente, o salto da
Matemática para dimensão 1 para a Matemática para a dimensão 2 envolve novas situações. Pelo menos temos mais
espaço para onde nos mexermos... surgem buracos, convexidades e não convexidades, coisas que não existiam
na simples dimensão 1.
Mas vamos aprender como manipular estas dificuldades novas, é o nosso objetivo.
Então, esquecendo por um momento que podem haver buracos nas superfícies, as integrais de superfície vão ser uma generalização das
integrais de linha: vamos parametrizar superfícies em retângulos do plano e o cálculo vai se proceder como numa integral dupla. Aos
poucos eu irei colocando novas dificuldades (ou soluções) na teoria, mas na lista complementar exer04b vou apenas abrir o horizonte
para começarmos o trabalho com integrais de superfície partindo da simples generalização: parametrizando uma superfície sobre um
retângulo e calculando a área da superfície.
Se você quiser ler um pouco a respeito, procure por "mapas e atlas" que é a forma de
parametrização adequada de superfícies para que você se vá preparando para o que vamos precisar.
As duas primeiras questões da lista 04b
Centro de massa é um problema interessante que somente tem sentido em dimensão maior do que dois, no espaço 3D.
Um pedaço de arame, solto
no espaço pode ter o centro de massa localizado fora do arame, isto tem o que ver com convexidade.
A definição do centro de massa (baricentro) é o valor médio integral.
Se um corpo for convexo o valor médio (baricentro)
se localiza em algum ponto dentro do corpo. Mas a recíproca não é verdadeira.

Há uma frase central no texto acima definindo baricentro, "a integral na equação (1) está mal definida...".
É preciso desmitificar as "integrais" para conseguir compreendê-las melhor com uma notação mais simples.
- Integral não é uma soma, mas generaliza a somas, é uma espécie de limite.
Vou recuperar um pouco da história que
você passou ao estudar integral.
- Primeiro era a área sob o gráfico de uma função, limitado pelo eixo OX - o domínio;
- Depois uma forma de calcular esta área lhe foi apresentada como uma soma de áreas de retângulos;
- Em seguida você viu que para aumentar a precisão era preciso reduzir a base dos retângulos, quer dizer era uma soma de alturas
contrabalançada com pesos (a base dos retãngulos). Se fosse somente a soma das alturas o valor iria crescer indefinidamente então
a multiplicação por valores cada vez menores produziu um equilíbrio: o limite;
- É possível comparar as integrais com matrizes e transformações lineares, nas integrais as funções que estão sendo integradas
funcionam como as matrizes da Álgebra Linear.
- Chegamos assim, (e eu sei que esta história ainda está mal contada...) a olhar as integrais como transformações em que as funções
que estão sendo integradas representam a deformação entre dois "ambientes" -
- o espaço de parametrização e
- uma certa variedade que está sendo parametrizada.
Embora esta história esteja mal contada é exatamente isto que são integrais em sua generalidade maior possível.
A integral que aparece na definição de baricentro é isto. A função f representa a deformação que o espaço de parametrização
sofre para representar f(A).
Se a função f for a identidade, então a medida de A é igual a medida de f(A), estamos translatando
ou "arrastando" A para uma posição no espaço.
Nas integrais aparece um "produto" f(x)dx porque na verdade este "produto"
representa uma derivada F'(x) de formas que o par ( "f(x)dx" , F(x)) sejam "derivada e primitiva".
Quando conseguirmos ver isto
claramente então não há nenhuma dificuldade no cálculo da integral. Quando não vemos isto com clareza então temos que produzir
transformações até obter este par e poder calcular a integral, usando o teorema fundamental do Cálculo,
e, nem sempre isto é possível.
Os dois primeiros exercício da lista 04b tem o objetivo de dar exemplos
desta transformação no cálculo do baricentro, que é uma integral
de linha.
A questão 03 da lista 04b
Nesta questão se pede que você construa regiões no plano para adquirir experiência
na visão de domínios sobre os quais serão calculadas integrais duplas. Este assunto
já foi mencionado na lista 02, entretanto aquela lista se limitou a domínios retângulares.
O objetivo agora é prepará-l@ para calcular integrais sobre domínios não retângulares. Esta
questão é um passo nesta direção.
A questão 05 da lista 04b
Trata de curvas de nível, derivada implícita e do gradiente.
São três conceitos que podem ser tratados em conjunto e que têm muito a ver um com o outro.
O meu objetivo nesta questão é passar esta idéia.
As curvas de nível são curvas situadas no domínio da função z = F(x,y) e correspondem, no domínio,
a um caminho sobre a superfície com altura constante. Quer dizer, se você construir uma
estrada sobre uma montanha seguindo uma curva de nível (a curva de nível não está na montanha...)
o resultado será uma estrada que nem subirá e nem descerá a montanha. Mesmo assim as curvas
de nível são um instrumento importante na construção de estradas: é se afastando de leve das curvas
de nível que se podem construir boas estradas para acesso às montanhas.
As curvas de nível se encontram no plano, no dominio de z = F(x,y) e representam um instrumento de
visualização das superfícies como mostram os gráficos feitos com gnuplot.


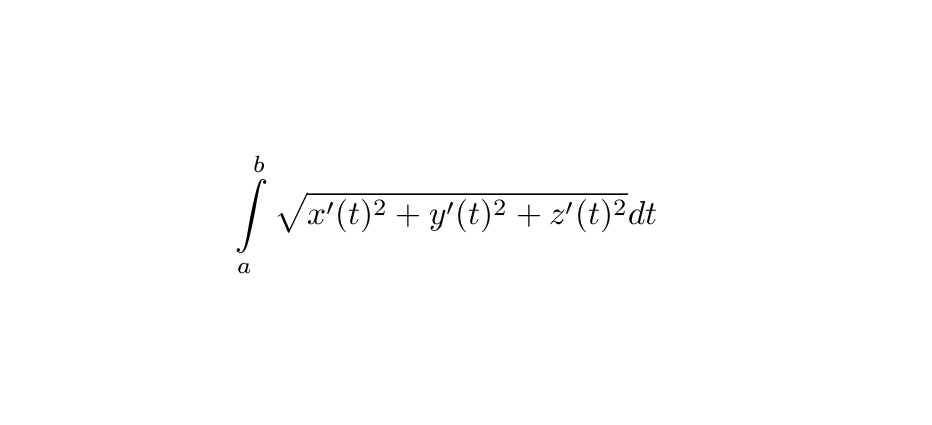
 gráfico interessante desta superfície dentro do círculo unitário- imagem de S1 .
gráfico interessante desta superfície dentro do círculo unitário- imagem de S1 .



