Plano tangente

Aviso: hoje, quarta-feira, 03 de Março, de 19:00 - 22:00 estarei atendendo por e-mail mas estarei na sala de aula de Cálculo II e também tirarei dúvidas no quadro para quem se fizer presente. Vou adotar esta sistemática nas quarta-feiras, o atendimento à distância se dará a partir da sala de aula, no horário indicado acima e de tarde, a partir do meu escritório, no horário de 15:00 - 17:00 horas.

Variedade

O termo variedade foi criado para romper a barreira tridimensional em que vivemos. Falamos em ponto, retas, planos, superfícies, volumes que são todos objetos que ficam dentro do limite da dimensão três. Embora pontos, reta, planos sejam invisíveis para nós seres tri-dimensionais, temos a sensação de que os conhecemos e entendemos.

As necessidades científicas muito além da dimensão três e precisam das dimensões 0,1,2 às quais não podemos ter acesso por razões físicas, de energia mesmo. Para isto, e para completar o vocabulário, criamos a palavra variedade que modificada por um adjetivo dimensional, resolve a questão linguística.

1. Um ponto é uma variedade de dimensão zero.
2. Uma reta é uma variedade linear de dimensão um. Aqui temos mais variedades, temos as variedades lineares e as variedades não lineares, de dimensão 1. Uma circunferência, a fronteira de um círculo, é uma variedade não linear de dimensão 1.
3. Um plano é uma variedade linear de dimensão dois. Aqui também temos mais variedades, uma esfera, a fronteira de uma bola, é uma variedade não linear de dimensão 2. Os planos são as variedades lineares de dimensão 2. Os parabolóides e os hiperbolóides, são variedades não lineares de dimensão 2.
4. Finalmente vem o mundo em vivemos, o tridimensional que é uma variedade linear de dimensão três contém o "batatóide" que habitamos, a Terra, a Lua, .... todos variedades não lineares de dimensão três. Depois das teorias da relatividade sabemos que não há variedades lineares e nem podemos perceber nenhuma variedade de dimensão dois por insuficiência energética, tanto nossa como delas. Mas fazemos um esforço de abstração e construimos me nossa mente os planos, variedades lineares de dimensão 2, ou dizemos que a luz de propaga em cima de uma superfíce (uma variedade não linear de dimensão dois) que localmente é um parabolóide ou um hiperbolóide. Mas o que é a luz, onda?
5. Falei acima "finalmente" mas todo o restante vem agora e é muito mais do que a dimensão três em que estamos prisioneiros embora consigamos romper esta prisão usando da abstração. Em geral saltamos direto para a dimensão infinita onde se encontram as ondas (eletromagnéticas) que se decompõem em ondas básicas do tipo y = sen(ax+b) - (y = cos(ax+b) é uma senoide também - mas as vezes usamos estas para tornar a nossas expressões mais bonitas).

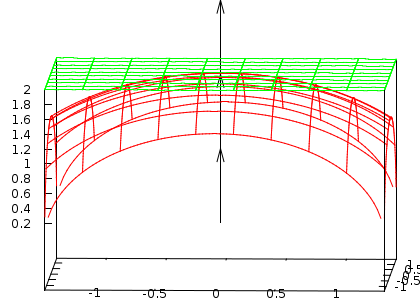
O que falei acima é um resumo violento do que podemos descrever em diversas disciplinas, mas serve como ponto de partida para seguirmos conversando. Não se intimede com a afirmação de que um resumo, se quiser discutir melhor o assunto, formule suas perguntas que elas podem gerar mais texto explicativo. Claro que não posso pretender ser enciclopédico e nem este será o objetivo. Experimente uma pesquisa com a palavra chave variedades não lineares para ver a riqueza do assunto, mas evite de se perder... Em inglês é manifolds. Inicialmente, nesta disciplina vou me restringir às variedades de dimensão dois, planos (variedades lineares de dimensão 2) ou as superfícies do tipo z = F(x,y) que frequentemente serão variedades não lineares de dimensão 2, como e o caso do gráfico que se encontra logo abaixo e que representa uma parte da fronteira de uma esfera.

Comparando o caso univariado e o caso multivariado

Quando uma função for diferenciável ela tem uma variedade linear tangente. Quando uma função univariada for diferenciável ela tem uma reta tangente em cada um dos seus pontos . Admitimos funções como diferenciáveis que possam ter alguns pontos onde elas não tenham variedade linear tangente, a função módulo é um desses exemplos, falha a existência de derivada na origem.

É aqui a comparação que desejo fazer, as funções bivariadas quando forem diferenciáiveis, tem um plano tangente. O mesmo se pode dizer com funções multivariadas, apenas temos que usar a palavra variedade linear tangente Mais para frente eu vou fazer esta comparação de forma mais geral. No momento eu vou me restringir ao caso das funções bivariadas.

O gráfico que aparece ao lado foi feito com gnuplot e o texto do

Neste gráfico, eu desenhei o plano tangente no ponto (0,0,f(0,0)) e você pode ver o vetor posição, que vai da origem até o ponto (0,0,f(0,0)) e também o vetor perpendicular ao plano tangente (sobreposto ao vetor posição). Desenhei também a tranlação do vetor tangente colocando uma das extremidades no ponto(0,0,f(0,0)). De formas que no desenho você pode ver três setas. Com gnuplot você pode visualizar este gráfico de forma muito melhor uma vez que você pode dar rotações o que lhe vai permitir entender melhor a posição do plano tangente relativamente á superfície que é a "casca de uma bola":

z = f(x,y) = sqrt( 4 - x**2 - y**2)

Esta equação veiu de

x**2 + y**2 + z**2 = 4

ao explicitar z. Esta última é a equação de uma esfera (a casca da esfera) no espaço 3D, tenho que explicitar z como função de x,y para que gnuplot possa fazer o gráfico. Esta não é a única forma de obter gráficos com gnuplot, depois veremos outras formas que são importantes para o Cálculo multivariado.

Leia o programa, a leitura deste programa aqui na página produz lixo no texto, você o irá ler melhor baixando do link "programas" onde ele se encontra exer03_01.gnuplot, rode o programa, considere-o com um laboratório, procure entender tanto o programa como as imagens que ele cria, e naturalmente me envie e-mail caso tenha dúvidas.

Por exemplo, troque a equação de

z = f(x,y)

e volte a rodar o programa.

Quando estudamos a equação do plano, fiz uma comparação com a equação da reta observando que na equação do plano havia dois coeficientes enquanto que na equação da reta apenas um coeficiente angular. Não houve ninguém que reclamasse que a equação geral do plano em 3D é

A(x-a) + B(y-b) + C(z-c) = 0

portanto, vizivelmente, com três coeficientdes. Também dizemos que a reta tem um coeficiente angular, mas a equação geral da reta é

A(x-a) + B(y-b) = 0

vizilmente com dois coeficientes. Como resolver esta contração?

É que nos interessa a equação colocada sob forma de função, em que explicitamos uma das variáveis.

1. No caso da reta, y = b + (A/B)(x-a) = f(x); - dividi por B, o coeficiente de (y-b).
2. No caso do plano, z = c + (A/C)(x-a) + (B/C)(y-b)=F(x,y); dividi por C, o coeficiente de (z-c).

Aqui intervém um hábito, uma convenção, no caso univariado costumamos explicitar y como função de x.

No caso multivariado, explicitamos z como função de (x,y). Esta convenção tem vários aspectos positivos, entre eles o de permitir que falemos uma linguagem comum o que nos permite de ler com facilidade os trabalhos de outras pessoas e assim facilitar a colaboração científica.

Quando explicitamos uma das variáveis, ficou claro que precisamos, na equação do plano apenas de dois coeficientes, matamos assim a contradição! Da mesma forma como eu adotei a equação da reta no padrão

y = b + m(x - a)

produzindo a expressão

y = f(a) + f'(a)(x-a)

para equação da reta tangente ao gráfico de y =f(x), vou também adotar o padrão

z = c + A(x-a) + B(y-b)

para equação do plano.

Observe que alterei a notação, o que acima era (A/C) agora é apenas A, e (B/C) é apenas B. Porque não precisamos do coeficiente "C".

Os dois coeficientes A,B são coeficientes parciais e representam o coeficiente angular do plano na direção do eixo OX ou do eixo OY, respectivamente. Aqui aparece o conceito de derivada parcial.

Continuando a comparação, a reta tem um único coeficiente angular que também é a sua derivada constante:

y = f(x) = b + m(x - a) ===> f'(x) = m

é a derivada constante de uma função do primeiro grau.

Num plano há muitas retas com uma infinidade de coeficientes angulares possíveis, mas há dois coeficientes padrão, um na direção de OX e outro na direção de OY: Qualquer outro coeficiente angular sobre o plano pode ser obtido como combinação linear destes dois.

Este é um conceito da Álgebra Linear que se encontra intimamente ligado com o conceito de dimensão, na dimensão dois, (que é o caso de um plano, uma variedade linear de dimensão dois) duas informações básicas são suficiente para descrever tudo num espaço de dimensão dois (ou quase tudo...).

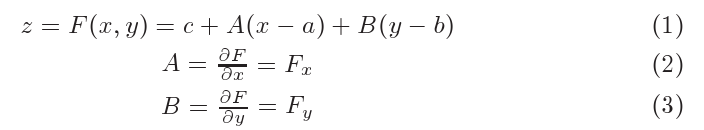
Esta é notação matemática para as "derivadas parciais" . Nas equações (2) e (3) acima você pode ver uma notação mais concisa, usando apenas o índice "x" ou "y" para indicar as derivadas parciais.

A forma de obter estas derivadas consiste em derivar, usando as regras habituais de derivação, com a restrição de que a outra "variável" é uma constante. Por exemplo, no caso da derivada parcial com respeito a "x" consideramos "y" uma constante. Qual é a justificativa para esta forma de cálculo? estamos fazendo uma restrição à função z = F(x,y) considerando apenas "x" como variávele, estamos nos restringindo a uma reta paralela ao eixo OX e neste momento o valor da segunda coordenada, "y" é constante.

Da mesma forma procedemos no cálculo da derivada parcial relativamente a "y", considerando "x " uma constante.

Derivação implícita

Quero lhe apresentar um instrumento muito importante e que vai nos levar de volta, de uma forma muito austuciosa, ao plano tangente, é a derivada implícita.

Vou começar por construir a derivada implicita no caso das funções de uma variável, sempre pensando de que a generalização, para o caso das funções bivariadas será um pequeno passo.

Considere a equação y = f(x) de uma função bivariada, analise os cálculos seguintes:

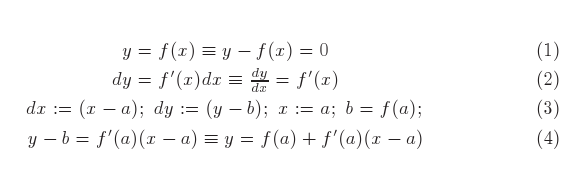
primeiro considerei a equação y - f(x) = 0 em que derivei todos os termos relativamente à variável presente e porisso escrevi dy indicando que havia derivada relativamente á variável y e depois derivei a expressão f(x) relativamente à variável x produzindo f'(x)dx . Observe que a derivada de y relativamente a y é 1, portanto alí está escrito 1dy e como de hábito escrevemos apenas dy.

Obtive assim a expressão

dy = f'(x) dx

1. dx := (x-a);
2. dy := (y-b);
3. x := a;

Vou fazer o mesmo com a equação z - f(x,y) para obter a equaação do plano tangente ao gráfico desta função no ponto (a,b,f(a,b)).

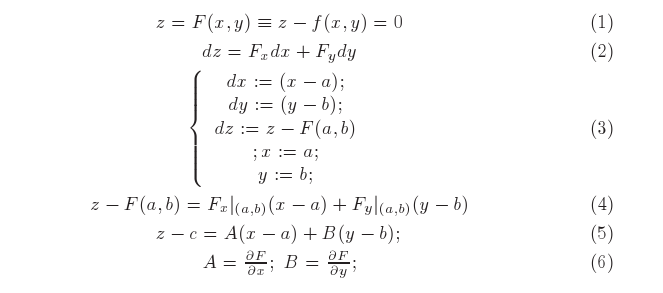
Fiz exatamente o mesmo que no caso univariado, derivei cada expressão relativamente às variáveis presentes, no cado da expressão F(x,y) isto produz uma combinação linear das derivadas parciais com os símbolos dx, dy indicando em cada caso relativamente a quem foi feita a derivação. Esta indicação é fundamental quando estivermos trabalhando com uma expressão "algébrica". Olhe este exemplo

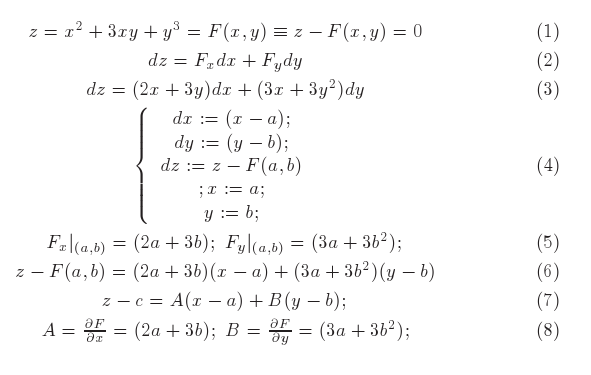
Coloque os dados num script do gnuplot e verá o plano tangente aparecer no ponto de tangência (a,b,F(a,b)) que você escolher. Isto já representa um forte indício de que tudo está perfeito, programas respondem á expressões formais corretas e servem para validar os cálculos que fizermos, sem dúvida isto é verdade. Mas vamos analisar o que foi feito.

Neste novo método de derivação, a derivação implícita, você tem a derivação que já conhecia, apenas aplicada a uma expressão em que estamos derivando por inteiro. Dissemos que deixamos indicativos sobre que tipo derivada estava sendo aplicada, relativamente a x ou relativamente a y com os símbolos dx, dy. Criamos assim um modelo de expressão à qual aplicamos um algoritmo que está expresso acima na equação de número (4) que nos permitiu deduzir do modelo a equação de um plano. Os coeficientes parciais desta plano são exatamente as derivadas parciais da função z = F(x,y) relativamente à cada uma das direções OX ou OY.

Vou escrever agora o script para gnuplot para que você raspe e cole e veja aparecer os gráficos de

z = F(x,y)

e do plano tangente num ponto que vou escolher. Altere você o ponto para ver outros gráficos.

F(x,y) = x**2 + 3*x*y + y**3;

DFx(x,y) = 2*x + 3*y; ## derivada parcial relativamente a x

DFy(x,y) = 3*x + 3*y**2; ## derivada parcial relativamente a y

a=2; b=-3; c = F(a,b); ## ponto escolhido --- altere aqui os valores de a,b

A = DFx(a,b); B = DFy(a,b); ## valor das derivadas parciais no ponto

P(x,y) = c + A*(x-a) + B*(y-b);

splot F(x,y), P(x,y)

print "Aperte enter para terminar"

pause -2

É importante observar que cálculo feitos corretamente conduzem a um programa que funciona de forma adequada, que sirva isto para estimulá-l@ a dominar a arte de fazer contas. Este script se encontrará, dentro de alguns minutos, no link "programas" da página, aguarde!