Vou mostrar-lhe como podemos calcular o comprimento de um caminho sobre uma superfície. Vou usar como motivação o caminho que a luz segue no Universo, mas o meu objetivo aqui não é fazer Física, apenas usar a Física como pano de fundo para uma construção geométrica, motivação enfim.
Mas sinta-se convidado para aprofundar a discussão sobretudo se isto criar condições para o aprendizado. Não sou um físico, e que vou discutir aqui de Física é aquilo que qualquer cidadão tem que entender desta ciência, como de qualquer outra ciência, como cultura geral. Então aqui sou amador ou autodidata.
A luz, como qualquer outra manifestação de energia, se propaga em todas as
direções e desta forma o dectamos como luz é a intensidade numa
região esférica, apenas "concentramos esta informação" num ponto
representativo da região.
O Cálculo vai nos dar mecanismos para interpretrar melhor esta "concentração
de informações" mas neste momento vou assumir um ponto de vista um pouco
distorcido com um objetivo imediato, vou interpretar a luz como uma
partícula em movimento ao longo de uma curva que fica sobre uma
superfície. Então, vou reduzir todo o problema ao estudo de curvas sobre
superfícies (se soubermos sobre que superfície trafega a luz, poderemos
calcular a distância entre a fonte e o receptor...e isto ninguém sabe, apenas
se constroi aproximadamente usando as fontes de energia gravitacional
conhecidas como poderia ser esta superfície). Podemos assim calcular a
distãncia relativa entre os corpos celestes... a distância que podemos medir
é o comprimento da curva que luz percorre no Universo uma vez que é a luz o
meio por onde nos chegam as informações sobre os corpos no Universo.
Eu cito, no texto, alguns programas, todos os programas citados se encontram no link "programas" da página da disciplina e podem ser livremente baixados, usados e modificados.
Uma curva é uma representação de um intervalo no espaço. Lembre-se do que eu fiz nas listas 05, 06 quando defini uma transformação para codificar um disco em cima de retângulo. Retângulos são objetos geométricos mais simples do discos, da mesma forma como intervalos são objetos geométricos mais simples do que curvas.
Em suma você verá que o nosso objetivo é representar uma classe grande de objetos geométricos (codificá-los) usando objetos mais simples: segmentos de reta (intervalos), retângulos, paralelepípedos...
A linguagem técnica que se usa é parametrizar em vez de codificar, e vou passar a usar esta palavra de agora em diante.
Você já encontrou as equações paramétricas de uma reta no espaço, e nas listas 05, 06 você encontrou as equações paramétricas (coordenadas polares) do círculo. As equações paramétricas nos permitem uma grande variedade de "representações" e gnuplot está muito bem equipado para nos forneceer as visualizações das equações paramétricas. É preciso fazê-lo entrar no modo paramétrico com os dois comandos. Mas há dois comandos para fazer gnuplot entrar no modo de equações paramétricas:
set parametric ## para entrar no modo paramétrico
set dummy t ## para definir a variável de parametrização como sendo t, desnecessário, é o padrão
Observe que estou usando a sintaxe do gnuplot quando eu escrever comandos, por exemplo acima, estou incluindo comentários, se você raspar e colar no terminal do gnuplot ele irá entender o comando e ignorar o comentário. A partir de agora gnuplot sabe fazer gráficos de curvas ou superfícies usando equações paramétricas. As questões 1 e 2 da lista 07 tem o objetivo de conduzí-lo a fazer gráficos de curvas usando equações paramétricas. Altere as equações dadas para obter outras curvas e assim ganhar mais intuição.
Nas listas 05,06 eu usei equações paramétricas chamadas "coordenadas polares" que funcionam de forma um pouco diferente das equações paramétricas que usadas agora nas questões 1,2 da lista 7. Agora o par de coordenadas representa raio e ângulo, nesta ordem. Muitas vezes estas duas coordenadas são usadas com a letras gregas rho, teta - foi este o uso nas listas 05, 06.
Gnuplot não usa esta denominação. Apenas entra no modo de coordenadas polares quando você utiliza o comando "set polar". A partir deste momento a variável t representa ângulo e qualquer função f(t) representa
r = f(t)
Na questão 03 estou lhe mostrando como usar o método do gnuplot e
Por exemplo
vai fazer o gráfico de três círculos de raios 1,2 e 3.
vai fazer o gráfico de uma curva em que o módulo (raio) e o ângulo crescem juntos com t o resultado é uma espiral.
o resultado é a mesma espiral que foi obtida no caso anterior.
Observe que são dois métodos diferentes, é preciso não confundí-los. Mas se você os confundir verá gráficos errados então tudo que você deve fazer é corrigir o que estiver fazendo. Sem estresse, você está aprendendo a usar gnuplot!
A questão 03 da lista 07 usa coordenadas polares com estas duas formas e conduz gnuplot a entender os dois métodos. Os dois itens finais desta questão tratam das coordenadas esféricas que um sistema de coordenadas semelhante às coordenadas polares para o espaço 3D.
Vou explorar na questão 4 as curvas de nível. Curvas de nível são curvas desenhadas no domínio de f e não no graf(f). Não ficam na superfície que é o gráfico de f, mas sim no domínio. É isto que as faz úteis para os cartógrafos ou engenheiros civís.
Olhe para uma montanha que tenha uns 500 m de altura sobre o nível do mar, e considere nele o nível 300m, quer dizer, a montanha cortada por um plano de altura 300m. Isto daria uma curva (supondo que a montanha é uma superfície, não um sólido!). A projeção desta curva no solo é a curva de nivel 300m.
Este método é usado pelos cartógrafos ou pelo engenheiros quando desejam representam numa folha os relevos da região á volta, então usam um instrumento, o teodolito, para registrar as mesmas altura - curvas de nível, numa folha de papel. gnuplot é bom para representar as curvas de nível de uma superfície.
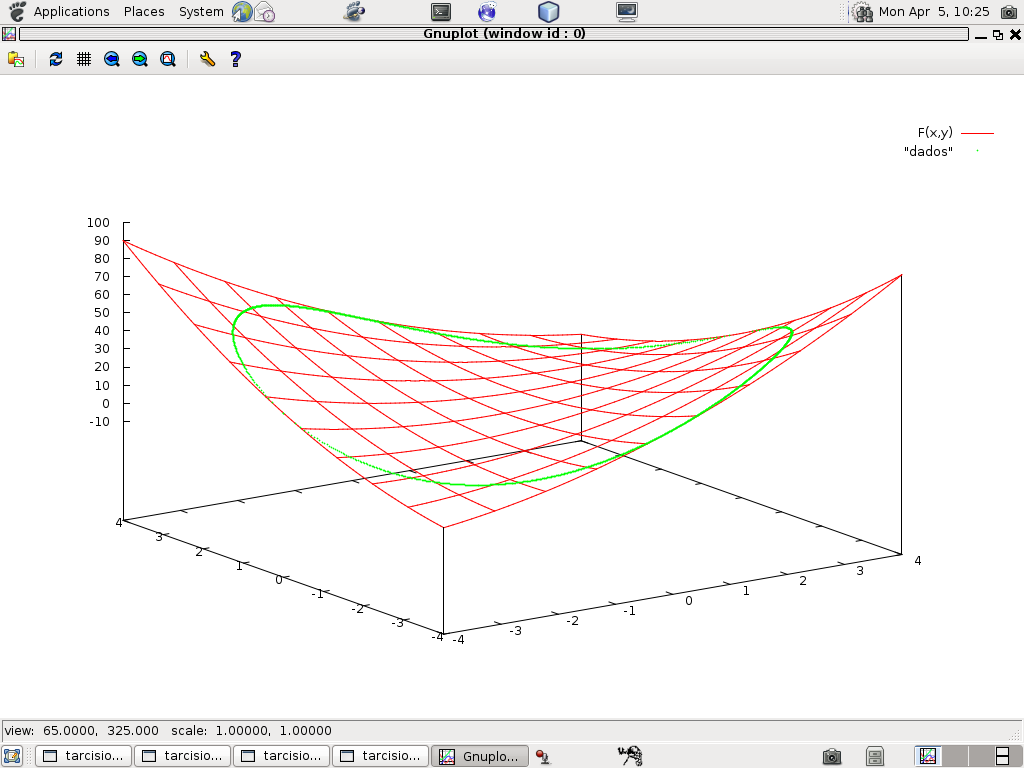
Um bom texto para que você se desenvolva no uso de gnuplot é este livro escrito pelo professor Maurício Galo. Na página 24 deste texto você encontra um exemplo de uso de curvas de nível.O programa exer07_05_a.calc cria imagens de curvas na superfície graf(F), você tem que fazer alterações no programa para obter a imagem da curva que você desejar.

A figura mostra a imagem de um círculo sobre o gráfico de F(x,y) = x**2 - 3xy + y**2 e no próximo gráfico se encontra a imagem de segmento de parábola.
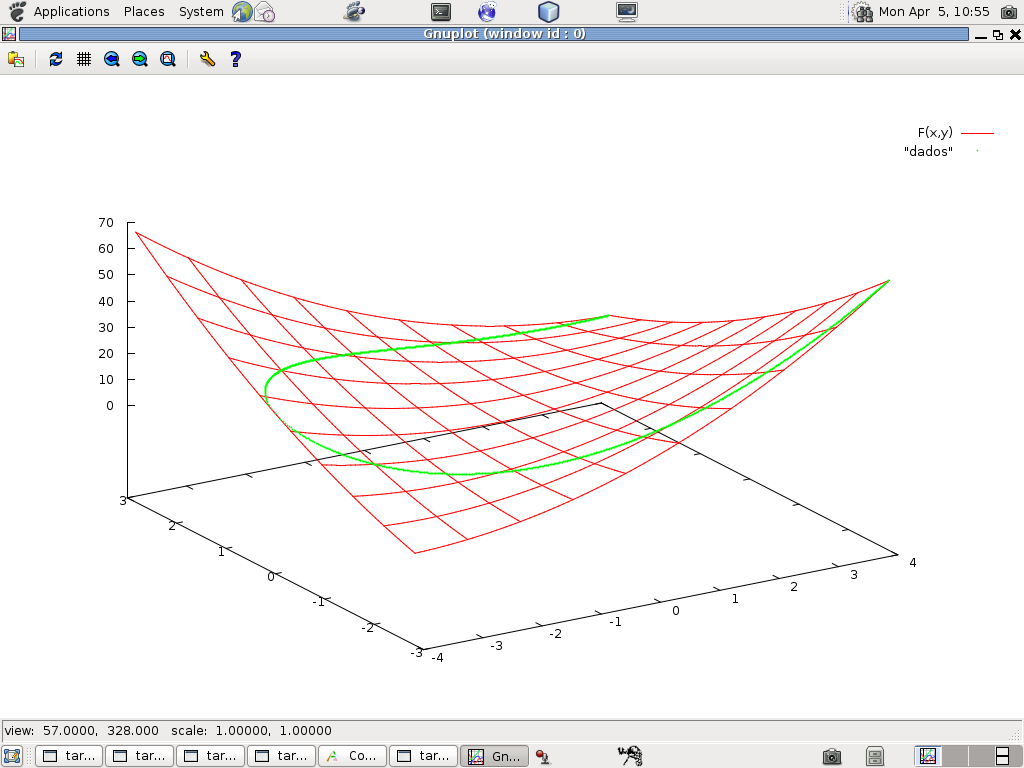
Porém o que nos interessa é que um avião saia de um ponto escolhido e chegue a outro ponto também escolhido, e este é um problema realmente difícil - selecionar a curva mais curta - estou chegando no assunto prometido, comprimento de curva - ligando dois pontos selecionados. Não sabemos fazer isto exatamente, a única solução é aproximada! Este é um problema de (elementar) de Cálculo Variacional.
Os programas exer07_05_a.calc e exer07_05_c.gnuplot se encontram no link "programas". O script para gnuplot foi gerado pelo programa em calc e depois eu o mofiquei para obter as figuras
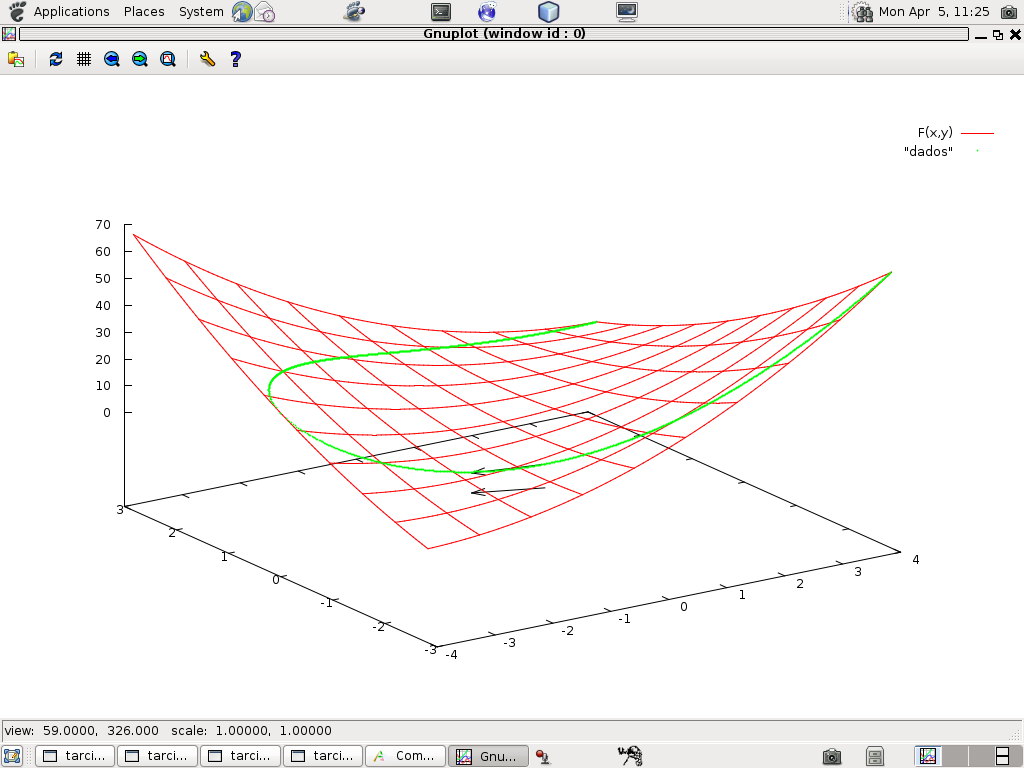
No próximo gráfico dei uma rotação para que você possa ver que um dos vetores se encontra no domínio e é paralelo ao vetor tangente ao gráfico da curva que se encontra na imagem de F.
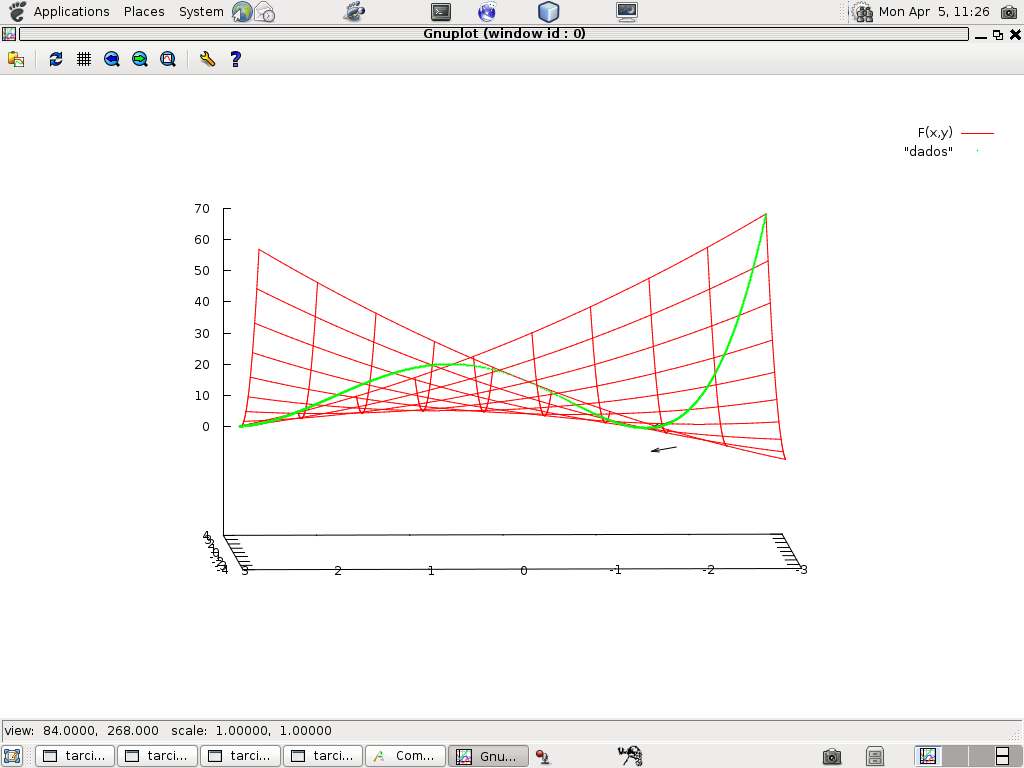
Eu obtive estes dois gráficos modificando o script para gnuplot produzido pelo programa em calc. É mais fácil construir um script "básico" com calc e depois modificá-lo para conseguir os efeitos desejados. Em aula, hoje, eu vou repetir esta construção.
Queria insistir: você não faz o programa se não souber Cálculo! Claro, você também não faz o programa se não souber programar! Porém, saber programar não conduz ao programa, e sabendo Cálculo você pode aprender facilmente a, pelo menos modificar, um programa de forma adequada.
Os itens da questão 5 testam sua compreensão destas transformações. Observe que há algo merece atenção na fórmula da 5-e), claro que F é derivável, por hipótese, mas... seria mesmo assim?
Este é um texto de apoio à lista 07, a lista se encontra no link "exercicios" da página da disciplina.