A derivada

Palavras-chave: derivada parcial, derivada, função multivariada, equação do plano, Jacobiana, plano tangente

Interpretação geométrica da derivada

O meu objetivo é mostrar-lhe que para as funções diferenciáveis de duas variáveis, o plano tangente representa uma generalização do que a reta tangente representa para as funções univariadas.

reta tangente e plano tangente

Vou evidenciar as semelhanças entre as equações da reta e do plano, porque no plano conseguimos fazer gráficos bem simples e bem claros, mas no espaço a clareza nos gráficos é muito dificil de ser alcançada.
Uma expressão como
y = ax + b = f(x),
no plano, representa uma reta, porque a taxa de variação de y em relação a x é constante. Quer dizer, se

x ----> x + Delta

então

y(x) ----> y(x+\Delta x) = f(x+\Delta x)

de tal modo que

y(x+\Delta x)-y(x) =f(x+\Delta x) - f(x) = \Delta y = a \Delta x.

Em palavras, a taxa de variação na horizontal (x) se transforma numa taxa de variação na vertical (y) com na meama proporção a, que é o coeficiente angular da reta.
O coeficiente angular na equação da reta,a é a taxa de proporcionalidade. Todos os triângulos retângulos, com hipotenusa sobre uma reta e catetos paralelos aos eixos coordenados, são semelhantes, e a razão de proporcionalidade entre os seus catetos é o coeficiente angular da reta que corta as paralelas, como podemos ver na figura.

paralelas cortadas por uma transversal

Não conseguiremos dizer nada tão simples com planos no espaço, e menos ainda conseguir gráficos como este.

Uma outra forma de repetir o que foi dito acima é: ``se construirmos uma progressão aritmética de razão Delta com a variável x, produziremos a progressão aritmética de razão a Delta com a variável y''. É o que a figura lhe mostra.

A consequência disto é que se o gráfico de f contiver qualquer progressão artimética do tipo mencionado acima, então f é a equação de uma reta.
E, reciprocamente, como numa reta podemos considerar qualquer progressão aritmética, todas com a mesma razão (o coeficiente angular da reta), então a equação de qualquer reta é da forma

y = a(x-x₀) + b₀

O número a é a derivada constante de f

Definição:

f'(x) = a

Se considerarmos, agora, a expressão (equação de um plano)

(E) z = g(x,y) = a(x-p) + b(y-q) + r,

Observe as semelhanças com a equação da reta. Esta é a equação de um plano que passa no ponto (p, q, r) - verifique isto fazendo simultaneamente

x = p; y = q;

Ela irá representar também uma figura de tipo linear, porque, se g for associada a progressões aritméticas das variáveis x ou y, separadamente ou em conjunto, correspondem progressões aritméticas da variàvel z com razões obtidas pormultiplicação pelos coeficientes a, b:

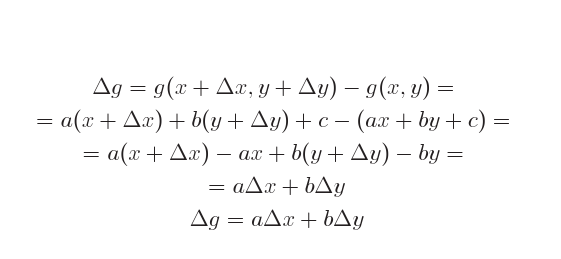
combinação dos coeficientes parciais

Estamos sobre um plano, o gráfico de z = g(x,y).
Se nos movermos na direção OX as progressões aritméticas serão de razão a.
Se nos movermos na direção OY as progressões aritméticas serão de razão b.
Desta forma chamamos as duas taxas de variação de parciais, e algumas vezes dizemos, a taxa de variação na direção de OX é tomada deixando a variável y constante, ou, reciprocamente, a taxa de variação na direção de OY é tomada deixando a variável x constante.
Como no caso da reta, os números a,b que aparecem nas equações acima são derivadas, como são calculadas na direção OX ou na direção OY, separadamente, são chamadas derivadas parciais:

derivadas parciais

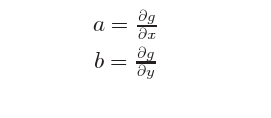
é a notação que usamos em Matemática para as derivadas parciais.

Podemos escrever de uma forma mais sofisticada estes cálculos

O produto que agora aparece é um produto de matrizes.

E se z = g(x,y) for uma função qualquer (diferenciável). Diferenciável significa que tem uma aproximação linear, que tem um objeto linear tangente.

No caso das funções univariadas: uma reta tangente.

No caso das funções bivariadas: um plano tangente.

Este é o significado de que uma função seja diferenciável.

No caso das funções univariadas, a reta tangente é a aproximação linear que e a sua equação representa o primeiro passo da Fórmula de Taylor:

y = f(x) ==> P(x) = f(a) + f'(a)(x - a)

Vamos ver como fica no caso bivariado, z = g(x,y) em que g é uma função derivável, quer dizer, tem um plano tangente em qualquer ponto do seu gráfico

(x,y, g(x,y))

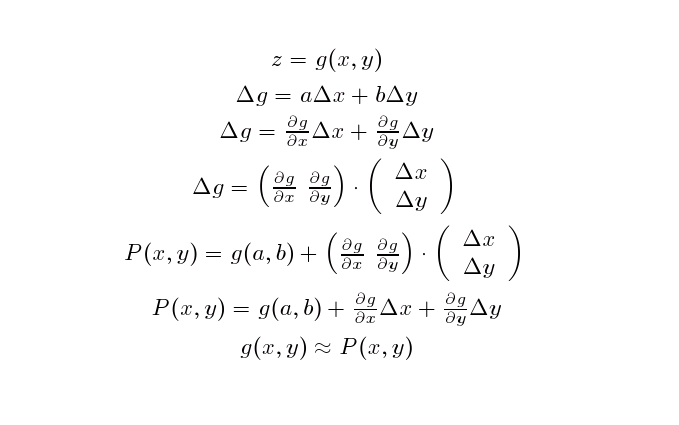
produto de matrizes

Com isto generalizamos imediatamente os càlculos que fizemos no caso da equação da reta. Também temos a primeira versão da Fórmula de Taylor para o caso das funções bivariadas - a equação do plano tangente no ponto

(a,b,c) = (a,b, g(a,b))

Os cálculos que estão feitos acima representam uma nova forma de multiplicar, um produto de matrizes, que é uma nova forma de multiplicar.

Se abstrairmos a forma particular do coeficiente multiplicativo e da variável, podemos ver estas contas como

produto de matrizes

As contas que podemos ver acima representam dois casos:

quando g for uma função linear - observe a igualdade.
quando g não for uma função linear - observe o indicativo de aproximação.

quando estão propositalmente repetidas para que você tenha os cálculos feitos de diferentes formas. Compare as equações (6) e (8) elas mostram a diferença nos dois casos. A equação (9) tem exatamente a forma da equação da equação da reta, ela é a expressão de uma equação linear emqualquer dimensão: um, dois, três, etc...

z = Ax + x₀

apenas o coeficiente multiplicativo agora é uma matriz.

São estas semelhanças que fazem-nos avançar em ciência, com elas damos os saltos para novos conceitos. É preciso aprender a ver as semelhanças para adquirir uma nova visão. Aqui você está sendo convidado a entender o que acontece no espaço 3D a partir de semelhanças com o espaço 2D.
A matriz, formadas dos coeficientes parciais, é, para a equação do plano aquilo que o coeficiente angular é para reta: a derivada.

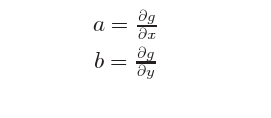
Os coeficientes desta matriz são as derivadas parciais da função g:

derivadas parciais

Leitura:

Chamamos estes dois coeficientes parciais,

"derivada de g com respeito a x" ;
"derivada de g com respeito a y";

Aqui você pode ver uma complicação introduzida pelos nossos antigos que não conseguiram perceber que a derivada era a matriz.
Eles primeiro entenderam que havia "derivadas parciais" e somente com o tempo é que conseguimos entender que na verdade a derivada era matriz, a matriz das derivadas parciais, ainda chamada Jacobiana J(g).

A equação (9), no conjunto de cálculos feitos logo acima, é a equação do plano que passa pelo ponto

(p, q, c) = (X₀, c) = (p,q, g(X₀) )

do espaço 3D = R³ e

AX₀ + c = z_o = g(p,q)

é o valor de g no ponto X₀ = (p,q).

Plano tangente ao gráfico de z = g(x,y)

Da mesma forma como quando uma função univariada y = f(x) tem uma reta tangente em cada ponto do seu gráfico, no caso das funções bivariadas,quando elas forem diferenciáveis, há um plano tangente em cada ponto do gráfico.
No caso bivariado os coeficientes são multinúmeros, as matrizes.
Buscamos com as generalizações operar com conceitos mais complexos com a mesma formalidade com que operamos com os conceitos mais simples.
Esta é forma como conseguimos quebrar a barreira dimensional e falar de fenômenos multidimensionais com a mesma linguagem com que falamos dos fenômenos unidimensionais.

Generalização da reta tangente

Vou começar relembrando a equação da reta tangente ao gráfico de uma função diferenciável

y = f(x) no ponto ( a, f(a)) que você pode ver na

a reta tangente

Por comparação, vou apresentar a equação do plano tangente ao gráfico de uma função diferenciável z = g(x,y) no ponto (p,q, g(p,q)).
A equação da reta que passa pelo ponto

(a,f(a))
sendo tangente ao gráfico dey = f(x) neste ponto. Os cálculos são

(1) y = b + m(x - a)
(2) y = f(a) + f'(a)(x - a)

na equação (1) temos a equação da reta que passa no ponto

(a,b) = (a, f(a))

e tem coeficiente angular m.
Substituimos esta duas informações para obter a equação (2) que é de uma reta que passa no ponto (a , f(a)) e tem coeficiente angular m = f'(a).

Esta é a interpretação geométrica da derivada no caso univariado.

Observe que a equação da reta tangente é a primeira forma (caso) da fórmula de Taylor um polinômio de prmeiro grau tangente ao gráfico de y = f(x) no ponto (a,f(a)).

Vou fazer esta mesma interpretação geométrica para o caso bivariado, sem apresentar gráfico, mas vou escrever um script para gnuplot que lhe permitirá dar rotações no gráfico, usando o ratinho e ter uma visão, no caso bivariado, semelhante ao da figura univariada. Repetinido, para uma função bivariada, os passos que relembrei do caso univariado, a equação de um plano que passa no ponto (p,q,g(p,q)), é

(1) z - g(p,q) = a(x - p) + b(y - q); c = g(p,q);
(2) z = c + a(x - p) + b(y - q)
(3) P(x,y) = c + a(x - p) + b(y - q) ; P(p,q) = c = g(p,q);
(4) P(x,y) = P(a,b) + a(x - p) + b(y - q) ;
(5) P(x,y) = g(p,q) + (Dg/Dx)(x - p) + (Dg/Dy)(y - q) ;

Na equação (1) escrevi a expressão do polinômio do primeiro grau em duas variáveis e você pode ver que

P(p,q) = c

Fiz uma pequena modificação da equação (1) para obter a equação (2)
na equação (3) estou chamando z = P(x,y) .
Na equação (4) estou usando a expressão c como o valor de P no ponto (p,q).
Na equação (5) estou usando as notações (Dg/Dx), (Dg/Dy) para representar as derivadas parciais de g em relação a cada uma das direções, OX, OY.

que significa que o gráfico deste polinômio passa no ponto (p,q,g(p,q)).

O gráfico de um polinômio do primeiro grau em duas variáveis é um plano.

Como queremos que este plano seja tangente ao gráfico da função diferenciável

z = g(x,y)

então vamos impor as condições para que isto aconteça:

c = g(p,q);

para que o plano passe no ponto

(p,q,g(p,q))
(a) é derivada parcial de g relativamente a x; para que o coeficiente angular na direção do eixo OX coincida com derivada parcial de f nesta direção e,
(b) é derivada parcial de g relativamente a y; para que o coeficiente angular na direção do eixo OY coincida com derivada parcial de f nesta direção.

Estas contas em Matemática. Com este script do gnuplot você pode ver acontecer os gráficos com planos tangentes. Com o ratinho, é possível dar rotações nos gráficos e assim conseguir visualizar melhor os gráficos.
Acrescente os comandos

set xrange
set yrange
set zrange

para obter um gráfico mais preciso. Faça experiências para aprender a usar.

## a funcao g
g(x,y) = x**2 + y**2
## derivadas parciais
Dgx(x,y) = 2*x
Dgy(x,y) = 2*y
p = -2
q = 2
## equacao do plano tangente
Q(x,y) = g(p,q) + Dgx(p,q)*(x - p) + Dgy(p,q)*(y - q)
## comando do gnuplot para fazer graficos bivariados
splot g(x,y), Q(x,y)
pause -2
p = -5
q = 5
splot g(x,y), Q(x,y)
pause -2
q = -5
splot g(x,y), Q(x,y)
pause -2
## a funcao g
g(x,y) = x**2 - 3*x*y + y**2
## derivadas parciais
Dgx(x,y) = 2*x - 3*y
Dgy(x,y) = - 3*x + 2*y
p = -1
q = 1
## equacao do plano tangente
P(x,y) = g(p,q) + Dgx(p,q)*(x - p) + Dgy(p,q)*(y - q)
## comando do gnuplot para fazer graficos bivariados
splot g(x,y), P(x,y)
pause -2
p = -2
splot g(x,y), P(x,y)

Este script foi testado e se encontra dentro do programa (no link programas) exer02_01.gnuplot

O objetivo deste programa é de lhe fornecer um momento laboratorial. Com ele você pode ver gráficos de planos tangentes a distintos pontos do gráfico de uma função z = g(x,y). Tudo que você precisa fazer e alterar o valor do ponto (p,q) para obter o gráfico no ponto (p,q, g(p,q)), para as funções que estiverem definidas no programa.

Mas você deve ir além disto, altere também a equação da função para treinar-se no cálculo de derivadas parciais. Tenho insistido na idéia de que você deve adotar um livro texto - aquele que lhe convier. Faça os exercícios deste livro com a ajuda dos textos que estão oferecidos na página e inclusive use os programas que se encontram aqui como método de verificação dos seus cálculos.

Se os seus cálculos estiverem errados não irá aparecer nenhum plano tangente!