A palavra "campo" tem uma história significativa dentro das ciências físico matemáticas, por exemplo o potencial energético de uma fonte pode ser descrito pelo campo escalar que mede a sua intensidade. Estes termos pertencem à Física e foram absorvidos pela Matemática.
Vou tratar aqui de funções z = F(x,y), dos seus gráficos, de curvas que podemos traçar sobre a superfície graf(F) com o objetivo de discutir os problemas geométricos ligados a este tipo de superfície.
Os campos escalares são as funções definidas em
n
e tomando valores em
.
Na lista 03 discutimos o vetor perpendicular ao plano tangente que tem as derivadas parciais nas suas duas primeiras coordenadas e a terceira é 1 (ou -1) - observe os sinais! Relembrando, a equação de um plano que passa pelo ponto (a,b,c) é
A(x - a) + B(y - b) + C(z - c) = 0
Este é o plano que é perpendicular ao vetor (A,B,C).
Derivando implicitamente z = F(x,y) chegamos no modelo de objeto tangente (porque foi obtido por derivação)
dz = Fxdx + Fydy
e substituindo no modelo os diferenciais por diferenças, calculando as derivadas parciais no ponto (a,b) obtivemos a equação do plano tangente no ponto (a,b,F(a,b))z - F(a,b)= Fx(a,b)(x-a) + Fy(a,b)(y-b)
ou ainda
z - F(a,b) - Fx(a,b)(x-a) - Fy(a,b)(y-b) = 0
que evidencia o vetor perpendicular a este plano ( - Fx(a,b), - Fy(a,b), 1).
Ninguém perguntou porque a última coordenada é 1. Observe que a equação do plano representa um produto escalar de um vetor genérico do plano (x-a, y-b, z-F(a,b)) por vetor que é perpendicular a este vetor genérico, interpretado desta forma o vetor perpendicular é
(- Fx(a,b), - Fy(a,b), 1 )
Faça experiências com o programa exer04_01.gnuplot. Ele mostra, no ponto que você escolher, os vetores posição, e o vetor perpendicular assim como uma translação do vetor perpendicular para a posição de tangência. Este programa tem um pequeno texto teórico, não passe o texto sem o ler, e eu até diria, leia mais de uma vez até que estas idéias fiquem claras.E não duvide sobre fazer perguntas.
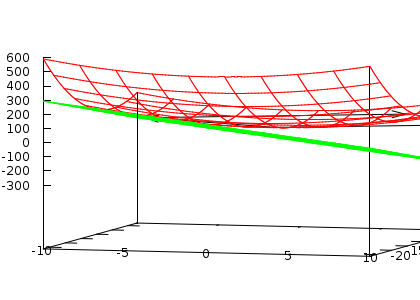
A figura ao lado foi feita com este programa , nela apenas podemos ver o plano tangente , as imagens dos vetores posição e perpendiular (ao plano tangente) estão obscurecidas pela imagem do gráfico da função. Mas rodando o programa você tem a oportunidade de rodar o gráfico no espaço e pode visualizar bem três vetores que este programa desenha:
O próximo gráfico, que você pode obter com o mesmo programa se ativar os comandos (desativados)
set xrange [a-15:a+15] ## para ativar, apague o sinal de comentário, ##
set xrange [b-15:b+15] ## no início da linha, mas não estes internos
set zrange [F(a,b)-20:F(a,b)+20] ## que você deve deixar.
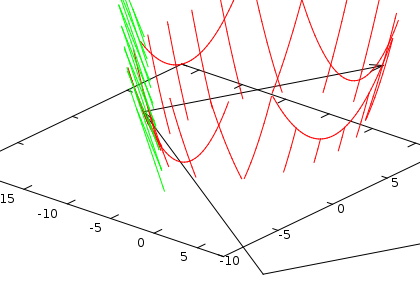
O gráfico ao lado foi feito com estes comandos ativados . Embora seja péssimo como gráfico,ele mostra claramente que há dois vetores paralelos, que é o vetor perpendicular (ao plano tangente) e uma translação deste vetor para o ponto posição de tangência.
Rodando o programa você pode fazer alterações no ponto de tangência e procurar uma imagem que lhe mostre melhor esta relação.
O meu objetivo neste capítulo é explorar vetores colocados em pontos de uma superfície para lhe dar um treinamento com as relações geométrico-espaciais entre os vetores
Ao final, vou simular um vôo de avião entre dois pontos dados. Uma rápida explicação (seria bom que esta explicação sumaria excitasse sua curiosidade e você procurasse ler mais a respeito, talvez fazendo uma busca na Internet pela palavra chave "piloto automático". Não espere que a minha explicação seja parecida com que a você vai eventualmente encontrar, neste assunto eu sou um "amador" e não um técnico de vôo (engenheiro de vôo). O meu objetivo aqui é mostrar como posso, com as ferramentas ainda rudimentares que estamos construindo, simular o vôo de um avião no "espaço aéreo " representado pelo gráfico de uma função z = F(x,y) e isto novamente está afastado da realidade, mas é o que disponho para usar.
Estou chamando de uma "situação real" uma simulação que vou fazer da realidade, usando expressões algébricas que representam, seguramente, uma péssima simulação da realidade. Mas é o que tenho disponível.
Quero lhe mostrar como traçar uma poligonal sobre uma superfície do tipo z=F(x,y) como um método para produzir um caminho sobre uma superfície. Estou usando uma poligonal para usar a idéia de aproximação. Não seria possível construir um caminho sobre uma superfície no espaço. Além disto esta idéia não seria prática. As razões que podem nos levar à construção de um caminho no espaço associado a uma determinada superfície estão ligadas a um campo vetorial sob o qual estejamos condicionados, por exemplo as forças produzidas pela movimentação de massas de ar na atmosfera e a necessidade de deslocamento de um avião entre dois pontos. O avião vai viajar num caminho sobre uma superfície que teoricamente seria aquela em que passa o "corredor" definido pelo sistema que gerencia o espaço aéreo, mas, deformado pela energia das massas de ar. O resultado é uma poligonal obtida pelas correções do piloto automático. Aqui estarei simulando situações "concretas" com uma equação algébrica.
Você pode argumentar que simular situações reais com uma expressão algébrica não teria validade e isto até certo ponto é verdadeiro. O que ocorre é que vamos usar em situações reais dos instrumentos que vou descrever aqui. Sem a formulação "algébrica" estes instrumentos não existiriam ou menos ainda nós poderiamos produzir uma metodologia pedagógica para treiná-l@ em seu uso. Então vou descrever o ambiente com uma equação do tipo z = F(x,y). O programa exer04_01.gnuplot faz esta simulação e você deve rodá-lo, e como sempre, eu o convido a alterá-lo usando-o como um laboratório para o seu aprendizado: troque as equações, as constantes (vetores) e volte a rodar o programa.
Vamos ao ponto alto da nossa aplicação de plano tangente. Entenda a razão do que estamos fazendo, o porque do plano tangente.Não duvide sobre fazer perguntas, isto pode me ajudar a melhorar este texto.
Vou usar uma função "algébrica" - não será algébrica porque vou usar uma senoide para perturbar o espaço e tornar o vôo do avião mais realistico! Colocar um avião viajando num paraboloide seria demasiado afastado da realidade, porque devido às correntes de ar quente (ou frio) o avião é "suavemente" jogado para cima e para baixo (certo, algumas vezes com alguma violência) então ou vou usar a função
z = F(x,y) = (x^{2} + y^{2})sin(xy)
para representar o espaço aéreo onde estarão dois aeroportos entre os quais uma das escalas do vôo vai se dar.
Porém os aviões usam propulsão para se mover no espaço, e embora eles sejam capazes de fazer pequenas curvas, não muito agudas, para esta minha simulação (ainda muito deficiente) eu vou usar poligonais. A teoria é a seguinte:
Repetindo, minha simulação não vai descrever decolagem e aterrissagem, estas etapas vai ficar para uma outra ocasião!
O programa exer04_01.gnuplot mostra como podemos construir uma poligonal sobre o plano tangente, rode e leia este programa. Esta simulação tem alguns defeitos que poderemos discutir posteriormente, uma delas, seria a escolha do melhor plano tangente (aquele que otimizasse energiticamente e sob o ponto de vista de tempo - logo também energeticamente - a rota do avião). Vou deixar de lado esta complicação importantíssima.
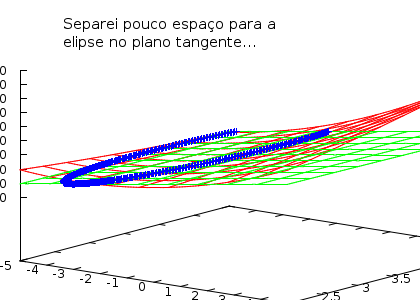
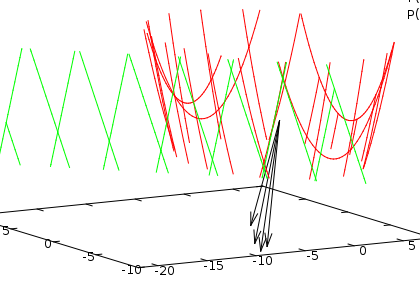 Na figura ao lado, produzida com o programa exer04_01.gnuplot, e
fazendo uma rotação com o ratinho, posse ver uma coleção de vetores que
foram obtidos com rotações em cima do plano tangente todos eles aplicados
(transladados) para o ponto (a,b,F(a,b)).
Na figura ao lado, produzida com o programa exer04_01.gnuplot, e
fazendo uma rotação com o ratinho, posse ver uma coleção de vetores que
foram obtidos com rotações em cima do plano tangente todos eles aplicados
(transladados) para o ponto (a,b,F(a,b)).
A tecnologia necessária está descrita no programa e consiste de usar coordenadas polares - isto significa trabalhar em cima de um círculo de raio especificado rho.
Dentro do prpgrama exer04_01.gnuplot você pode ler este texto: (copia da saída de dados do programa editado para melhorar a redação).
Uma forma de trabalhar com vetores que fiquem próximos de um ponto dado, consiste em colocar um círculo em volta do ponto desejado (no domínio da função) controlando a distância com o raio do círculo - raio pequeno, pontos muito próximos do centro.
Qual é a tecnologia necessária:
rho cos(alpha); rho sen(alpha)
alpha .
P(rho cos(alpha), rho sin(alpha))
é a imagem de um pequeno vetor, com direção escolhida, sobre o plano tangente.
Para construir a rota do avião vou considerar o fim de cada segmento de reta como o começo de outro construindo uma poligonal. Este é o objetivo da questão 5 na lista número 04.
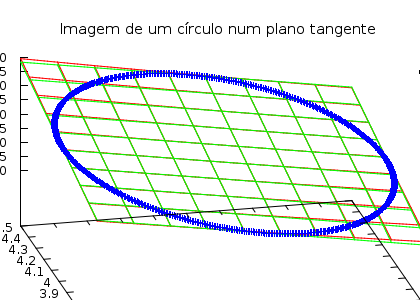
A imagem que você pode ver abaixo foi produzida com o programa exer04_05.gnuplot e você mesmo deve rodar o programa para obter imagens que você consiga manipular com o ratinho .

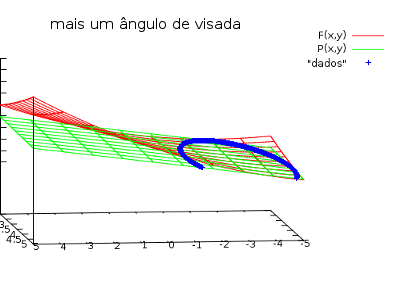
Mais abaixo você pode ver outra imagem obtida com uma rotação produzida pelo "ratinho" que também dá uma idéia das terríveis perturbações da região que o "avião" está atravessando. Basta que você altere a equação de z=F(x,y) para ver outras imagens menos perturbadas.
O objetivo inicial foi atingido, estou lhe mostrando como podemos colocar uma poligonal dentro do plano tangente.
Neste momento o que interessa é concluir que as contas que estamos fazendo tem sentido:
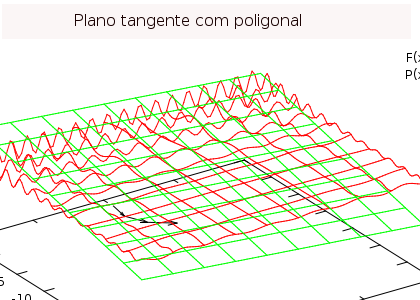
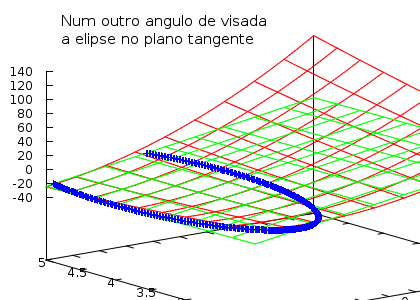
Deixo-lhe uma outra imagem ao lado mas você pode obter suas próprias imagens rodando o programa e inclusive alterando a equação da função. Estas modificaações serão um exercício interessante para treino no cálculo das derivadas parciais.
Estou abrindo o caminho para numa próxima lista procurarmos uma solução melhor, e é necessário ver que esta solução (para a rota do avião) não é a melhor. Qual é o defeito. Depois por que vamos investir numa solução de baixa qualidade.
Vamos por partes, primeiro a segunda discussão: investir numa solução de baixa qualidade.
Embora este solução seja de baixa qualidade que logo vou mostrar porque, ela é uma solução simples, porque vamos ficar inteiramente num mesmo plano tangente. E o que fizermos nesta solução mais simples vamos re-aproveitar quando complicarmos a solução.
Por que é uma solução de baixa qualidade? a aproximação linear de uma funçao somente tem valor, como aproximação, perto do ponto de tangência. Pense no caso do avião, se ele ficar no plano tangente durante toda a viagem (e isto é impossivel) ele cada vez irá se afastar mais da superfície terrestre - entraria em órbita, me vez de chegar ao próximo aeroporto. Vamos voltar a este problema em outra lista, veremos então que uma melhor solução vai se constituir de selecionar um novo plano tangente a cada passo. Portanto com um nível maior de complexidade. Chegaremos lá.
Eu fiz estas imagens com um programa escrito em calc, e estou terminando um programa em C++ para fazer imagens deste tipo que devo apresentar na aula de segunda-feira. Nelas eu projetei no plano tangente a imagem de um círculo centrado no ponto (a,b) com raio rho.